阅读 Casual inference_总结中

上一篇文章从概念的角度解释了因果推断中常见的问题，同时介绍因果图的分析方法来得到相关性信息和因果性信息流之间的方法。在这篇将更加深入的理解干预（Invention）、后门路径（Backdoor path）和后门调整（Backdoor adjustment）来准确的计算因果效应。以及假设较为困难的前门准则和 do 算子的方式来估计因果效应。这些方法的核心目的是：将因果估计转换成为统计估计，进而估计结果。

第四章、干预与后门调整

4.1 Do 运算符

注意干预 invention 和统计学中的 conditioning 之间的区别，为了表示区别因果中利用 do 算子表示

1. 统计中的conditional，指的是我们只将注意力限定在接受治疗的 subgroup 中
2. 因果中的 invention，指的是针对所有的群体添加干预

同时我们希望得到的结果是干预分布（interventional distributions）P（Y｜do（T）），同时也要注意干预分布和观测到的分布之间的区别。其中面临反事实的问题，那么什么样的情况下可识别？

如果可以将包含 do 算子的表达式（Casual estimation）还原成为没有 do 算子的表达式（statistical estimate），则说明是可识别的

因果机制（Casual mechanism）指的是，对于一个节点来说，影响其的结果只包含其parent 和对应的边。在因果机制的基础上，我们作出干预是局部的假设，我们假设对于一些变量的干预改变 X 对应的因果机制，而不是改变其产生其他变量的因果机制，也可以额被称为模块化（modularity），或者是独立机制、自主性和不变性机制。

干预操作的本质是希望改变原有的概率分布：

1. 第一种是观察数据中的因果图
2. 第二种是针对 T 施加干预的结果，对于其他节点的因果机制没有发生改变，而针对干预节点由于其因果机制发生了改变，因此可以对其parent 节点进行截断
3. 第三种与上述的情况保持一致

添加干预的好处是可以让概率发生变化，那么为什么需要将概率升变化呢？核心目的是让策略效应的计算可以更加的简单，通过模块化的假设可以让我们在计算联合概率分布中将干预的节点进行剔除，具体来说就是截断公式（Truncated factorization ）

针对下列经典的情况，我们可以计算在施加干预和不施加干预前后的输出

1. 干预分布 P(y|do(t)
2. 观测分布P(y|t)

通过计算可以发现核心在于 P(X) 和 P(X|T)之间的分布差异造成了观察结果和干预分布之间的问题

4.2 后门路径和后门调整

在因果图中，如果希望识别两个节点的因果关系我们希望可以截断两个节点直接非因果的关联，而非因果的关联主要是通过非阻塞路径（unblocked path）进行传递，If 我们可以阻断这些路径，Then 就可以在干预 T 的情况下估计出 T 对 Y 的因果效应，由此得到的后门标准为：

需要有一系列变量的集合造成了：

1. W 阻塞了所有 T 和 X 之间的后门路径
2. W 不会包含 T 的任何后台节点

在后门准则的基础上，我们找到了调整变量，进而施加干预得到准确的因果效应估计

一个实际的例子来计算：干预和非干预情况下 的因果效应估计

1. 第一种在施加干预的情况下，可以通过截断公式来得到 Y 对于 T 的效应识别
2. 第二种是在不施加干预的情况下，利用相关性公式得到 Y 对于 T 的识别，可以发现是存在有偏差的

在无法准确的施加干预的背景下，我们可以使用施加找到后门调整的变量来估算出因果效应

key point 总结

1. 为了计算干预之后的概率分布公式，我们可以使用局部性假设来对概率分布进行截断，进而计算出包含 do 算子下的因果效应分析公式
2. 因果关系识别的核心在于如何将包含 do 算子的公式转换成为没有 do 算子的表达式
3. 造成偏差的核心问题在于 P（X|T）和 P（X）之间的不一致造成的偏差
4. 如果我们可以找到后门调整的路径并进行截断，我们可以完成上述的操作

五、随机控制实验 randomized control experiments

在 AB 实验中，通过随机的控制策略的分发机制，可以保障最终得到的关联性为因果性。因为 T 和协变量直接完全独立是的最终的因果效应可以识别。

在随机对照实验需要保证 AB 两组是完全可比的，更加精确的定义这里的可比是各组的协变量之间的分布为相似的状态，确保协变量均衡是有效对比和分析后续的基础。核心是实现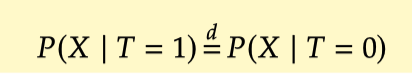，通过保证 X 和 T之间相互独立的状态，可以实现两者满足可交换的假设，进而准确的计算因果效应。如何实现协变量均衡可以从：

1. 随机化，在实验设计的过程中将变量随机的分配到不同的组别在满足条件
2. 匹配，通过匹配的方式来均衡协变量的分布
3. 统计套装，通过回归分析的方法对最终的结果进行纠偏的操作来调整对结果的影响 regression adjustment

六、非参数识别

6.1 前门准则

在第四章中我们在后门准则的基础上介绍了后门调整的方法（通过寻找到恰当的后门准则变量来实现后门调整，进而完成准确的因果效应估计），但是是否有其他的方式来实现因果效应的评估。或者说在之前的经验中我们尝试使用观察到充足的后门调整变量来实现因果效应的识别，但是如果在 W 无法被重插的情况下如何实现效应的评估。这里注重介绍 前门准则和前门调整。

前门调整适用于在后门准则的变量无法被充分识别和观察的情况下+中介变量可以被观察的情况下，可以通过三个步骤来计算出Y 中 T 因果效应

1. M 中 T 的因果效应，完全是因果关系
2. Y 中 M 的因果效应，可以通过对 T的后门准则的截断来完成
3. 联合上述两个步骤，来得到 Y 中 T 的因果效应

其中前门准则包括：

1. M 是充分的变量，也就是所有的因果路径均会通过 M 流向 Y
2. 所有 T 到 M 的后门路径均被截断
3. 所有从 M 到 Y 的路径均被 T 截断

6.2 do 算子

在不满足前门准则和后门准则的基础上，如何来实现因果效应的估计

附录

小角龙的学习记录- 04

因果发现的方法

因果发现的目的在于确定一个因果推的马尔可夫等价的方法，主要分为两种方式

1. 基于约束的方法，需要判定集合是否满足一系列假设检验（例如节点之间是否需要满足条件独立性假设），为了避免对于所有可能的子集合进行搜索，往往从一个全连接图开始逐渐增加条件集合的大小
2. 基于分数的方法，主要通过对模型类别进行假设限制，直接拟合一个结构因果模型架构来得到最终的打分函数的定义来进行求解。为了得到最优的因果图结果，需要包括两个部分：1. 最大化对数据的拟合程度、2. 对图结构的复杂程度进行惩罚。比如使用贪婪搜索的方法或者动态规划的方式。

因果估计和统计估计的方法

在假设后门变量均被观察到的假设的基础上，我们可以使用一系列的方法来进行纠偏的操作

1. s learner 和 t learner
2. tarnet 和 xlearner
3. PS 分数
4. double machine learning