CS229机器学习 贝叶斯学习理论 ｜ Vol7

[Andrew-Wu 基本理论01–贝叶斯学习（暨基本理论开篇）](https://blog.tjdata.site/2022/03/19/Andrew-Wu 基本理论01–贝叶斯学习（暨基本理论开篇）/)

Andrew-Wu 基本理论01–贝叶斯学习（暨基本理论开篇）blog.tjdata.site/2022/03/19/Andrew-Wu%20%E5%9F%BA%E6%9C%AC%E7%90%86%E8%AE%BA01–%E8%B4%9D%E5%8F%B6%E6%96%AF%E5%AD%A6%E4%B9%A0%EF%BC%88%E6%9A%A8%E5%9F%BA%E6%9C%AC%E7%90%86%E8%AE%BA%E5%BC%80%E7%AF%87%EF%BC%89/

0x00 计算学习理论的开篇

• 贝叶斯学习，贝叶斯推理提供来一种推理的概率方法，基于待考察的量遵循某种概率分布，且可根据这些概率及已观察到的数据进行推理得到最优的决策
• 集成学习，从多个弱学习器中得到一个较好的学习器
• 计算学习理论，致力于回答“在什么养的条件下成功的学习是可能的》”和“在 什么条件下某个特定的学习算法可保证成功运行？”，从近似正确（PAC）和对假设空间的自然度量两个角度来分析学习算法，在出错界限的框架下考察一个学习器在确定正确假设前可能产生的训练错误数量
• 基于实例的学习，每当学习器遇到一个新的实例，通过分析这个例子和之前存储的实例关系来将这个目标函数赋值给新的实例
• 基于解释的学习，先验知识用于分析观察到的学习样例是怎样满足目标概念的，然后这个解释被用于区分训练样例中哪些是相关的特征、哪些是不相关的，这样就可以基于逻辑推理进行泛化，而不是基于统计推理
• 增强学习，用来确定最优控制策略

0x01 贝叶斯学习简介

贝叶斯学习具有两个特点：第一，贝叶斯学习算法能够计算显始的假设概率，比如朴素贝叶斯分类器，是解决相应学习问题的最实际的方法之一；第二，为理解多数学习算法提供了一种有效的手段，这些算法不一定直接操纵概率数据

在机器学习中，通常最感兴趣是在给定训练数据D的时候，确定假设空间H中最可能的假设：

使用$P(h)$ 来代表没有训练数据前假设h拥有的概率，通常被称为prior probability（先验概率） $P(D)$ 代表将要观察的训练数据D的先验概率，也就是在没有某一假设成立时D的概率 $P(h|D)$ 代表的是看到训练数据D后h成立的置信度，这里是posterior probability（后验概率） $P(h|D)=\frac{P(D|h)P(h)}{P(D)}$ 极大后验（maximum a posterior，MAP）：$max P(D|h)P(h)$ 极大似然估计（maximum likelihood，MLE）：$max P(D|h)$

example：考虑一个医疗诊断问题，这里是h是是否患有癌症，这里是的数据是检测结果是正例+还是负例-

我们知道人群中患有癌症的概率是0.008；也就是没有患有癌症的概率是0.992

同时我们知道对于患有癌症的患者返回检测结果，0.98是+、0.02是-

对于没有患有癌症的患者，返回检测结果，0.03是+，0.97-

如果现在来了一个病人的检测结果是+，那么患有癌症的概率是多少

$P(h=患有癌症｜D=检测结果+)=\frac{P（D=+｜h=患有癌症）P（h=患有癌症）}{p（D=+|h=患）p（h=患）+p（D=+｜h=不患）p（不患）}=0.21$

example02～example03:

• 线性回归中极大似然和最小误差平方假设
• 逻辑回归中极大似然和交叉熵

0x02 贝叶斯分类器

基于一个简单而又强大的假设：在给定目标值事，属性值之间的相互条件独立，该假定说明在给定实例的目标值情况下，观察到的联合属性a1、a2、a3… 的概念等于单个属性的概率乘积： $$ P（a_1,a_2,…,a_n|h）=\prod P(a_i|h) $$ example：

我们是数据集和知道了关于一个🍉是否好坏的颜色和大小的属性：

对一个红色，大的🍉判断是否好坏：

P（好）=0.8

P（坏）=0.2

P（红色｜好）=0.8，

P（红色｜坏）=0.1，

P（大｜好）=0.9

P（大｜坏）=0.4

P（好）P（红色｜好）P（大｜好）=0.576

同理，观察到数据中坏的可能行=0.008

所以为好🍉

半进阶，需要考虑到独依赖估计（semi- naive bayes classifiers）

进阶：贝叶斯信念网

留个坑：贝叶斯分类器的文本估计

0x03 期望最大化算法（EM）

在讨论中，一直假设训练样本所有属性变量的值度可以被观测到，但是在实际中往往会遇到特征只有一部分可以观察到，EM算法可以用于变量从来没有被直接观察到的情况，只要这些变量所遵循的概率分布的一段形式

example：理解EM算法可以从一个实际的例子推导来得到，假设一个数据是从k个高斯分布混合而得到的，注意这个k未知，但是这个k个高斯分布的方差是$\sigma ^2$ 知道，现在需要预测是k个均值$<\mu_1,\mu_2,,,\mu_k>$,我们需要先假设均值的值，在重新估计隐藏变量的值来重新计算极大似然假设

Step01:当前的假设为$<\mu_1…,\mu_k>$ 的值，计算属于每个类别的期望值

$E(z=k|D)=p(x=x_i|\mu=\mu_i)/P(x=x_i)$

Step02: 计算一个新的极大似然假设，计算每个点属于每周类别的最大概率来更新均值，来替换称为新的假设

• 理论推导

对于n个样本观察数据${x^i}{i=1}^m$ 我们需要找到样本的模型参数$\theta$ 来最大对数似然函数，其中包含没有观察到的隐含数据Z $$ \bar \theta=argmax \Sigma log p(x^i;\theta)\ \bar \theta=argmax \Sigma log p(x^i,z^i;\theta)\ =\bar \theta=argmax \Sigma log \Sigma{z^i}\ p(x_i,z^i;\theta)\ =\bar \theta=argmax \Sigma log Q_i(Z^i) \Sigma_{z^i}\ \frac{p(x^i,z^i;\theta)}{Q_i(z^i)}引入一个新的分布\

=\Sigma\Sigma Q(Z_i) *log\frac{p(x_i,z_i;\theta)}{Q(z_i)}根据Jensen不等式 $$ 我们有许多的选择，但是这样Jesen会在后面的取常数的时候手链 $$ \frac{p(x^i,z^i;\theta)}{Q_i(z^i)}=c\ 同时\Sigma Q_i(Z^i)=1 $$ 由此可以看出 $$ Q_i(z^i)=p(x^i,z^i;\theta)/\Sigma(p(x^i,z^i;\theta))=p(z^i|x^i,\theta) $$ E: 计算$Q_i(Z^i)$

M: $argmax\Sigma\Sigma Q_i(Z^i)log(p(x^i,z^i;\theta)/Q_i(Z^i))$

EM算法的例子

更实际的例子：假设AB用相同的概率选择一个硬币，进行实验，每次都是独立的，请问如何估计两个硬币正面出现的概率？（a情况是知道选择硬币A还是B；b情况不知道选择硬币A还是B）

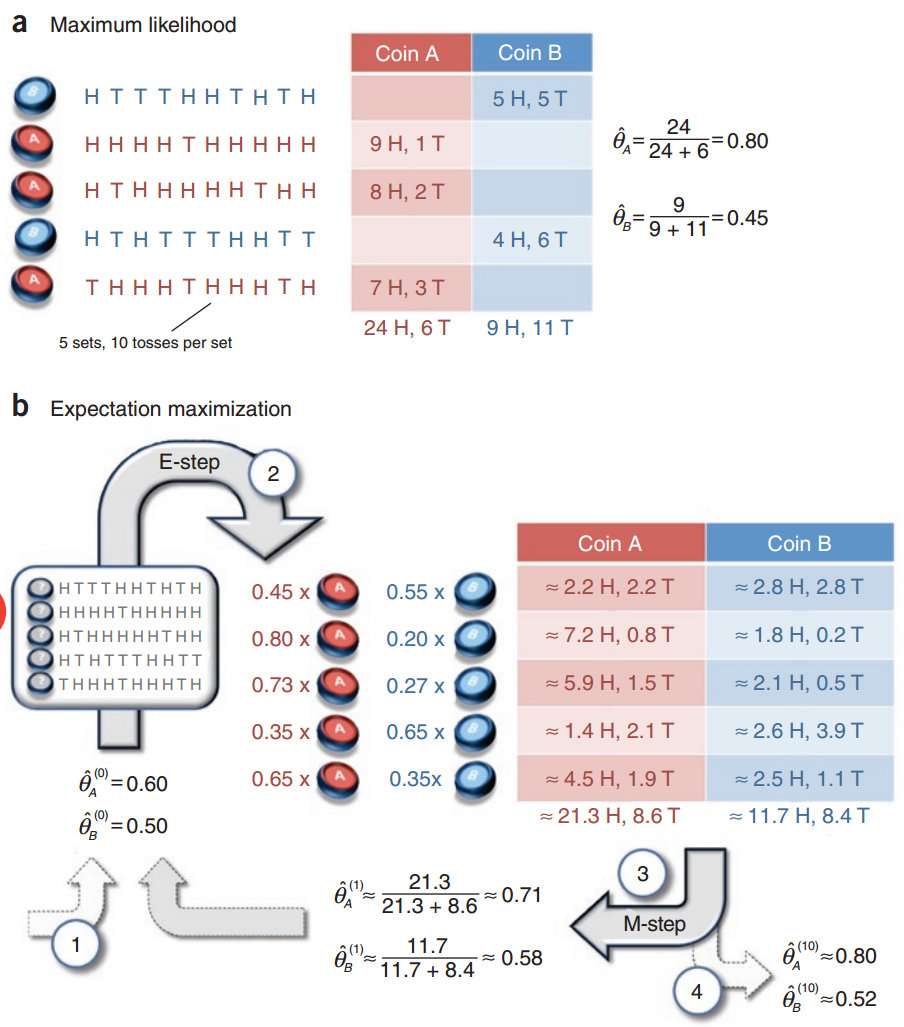
添加图片注释，不超过 140 字（可选）

E：我们假设A的概率是0.6；假设B的概率是0.5，这里仅仅是初始化的值，同时根据观测的数据来计算期望的分布 $$ Q_i(Z^i=A)=P（Z=A｜y_i,\bar\theta_A）=\frac{P（Z=A,y_i|\bar\theta_A）P(A)}{P（Z=A,y_i|\bar\theta_A）P(A)+P（Z=B,y_i|\bar\theta_A）P(B)}\ =[0.45,0.80,0.73,0.35,0.65] $$ Q: 其中的Q函数形式为 $$ Q(θ,θi)=∑j=1N∑zP(z|yj,θi)logP(yj,z|θ)=∑j=1Nμjlog(θyjA(1−θA)10−yj)+(1−μj)log(θyjB(1−θB)10−yj)] Q ( θ , θ i ) = ∑ j = 1 N ∑ z P ( z | y j , θ i ) l o g P ( y j , z | θ ) = ∑ j = 1 N μ j l o g ( θ A y j ( 1 − θ A ) 10 − y j ) + ( 1 − μ j ) l o g ( θ B y j ( 1 − θ B ) 10 − y j ) ]

$$ 求导来得到更新的$\theta_A,\theta_B$

比如混合高斯模型GMM、K-means聚类的方法

0x04 卡尔曼滤波

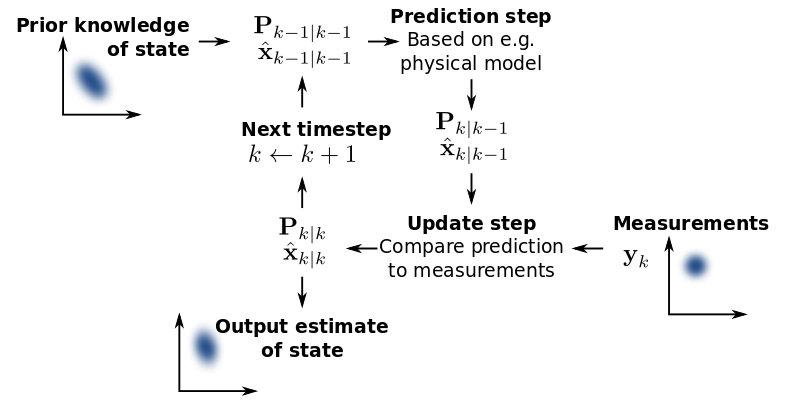
添加图片注释，不超过 140 字（可选）