CS229机器学习 SVM | vol2
讨论一种不同的线性分类和回归方法,每种学习算法都具有不同的归纳偏倚,做不同的假设,定义不同的目标函数,因此可能找到不同的模型 Support Vector Machine
0x01 引言
支持向量机使用Vapnik原则
不要在解决实际问题之前把解决一个更复杂的问题作为第一步(vapnik,1995)
训练后,线性模型的参数(权重向量)可以用训练集的一个子集表示,这个子集称为支持向量support vector。对于分类这些是靠近边界的实例,因此知道它们可以提取知识:这些事两个类之间的边界附近、不确定或有错误的实例,它们的个数给我们提供了范化误差的一个估计,并且正如我们将在下面看到的,能够用实例集表示模型参数进行核化
其总体框架:是一种分类算法,主要应用于二分类算法,通过定位两类数据在集合空间中的margin,来确定分类起,主要步骤分为:
- (建立模型)将二分类问题转换成为一个优化问题
- (求解模型)利用SMO算法、拉格朗日对偶、KKT条件来求解简化优化问题
- (分类讨论)之后利用松弛变量、核函数、惩罚因子等对不同情况下的优化问题进行求解
它的优点和缺点是什么?
- 优点:参数非常少,不像logistic regression还具有超参数,虽然比神经网络效果差,但是很简单
- 缺点:
0x02 建立模型
符号说明(notation)
$$ :等价于之前的𝑖𝑛𝑝𝑢𝑡:𝑋=(𝑥1,…,𝑥𝑛) 𝑙𝑎𝑏𝑒𝑙𝑠:𝑦∈−1,1 ℎ𝑦𝑝𝑒𝑟𝑝𝑙𝑎𝑛𝑒:𝜔𝑇𝑋+𝑏(等价于之前的𝜃𝑇𝑋) 𝑔(𝑍)={1 𝑖𝑓 𝑍>=0 −1 𝑖𝑓 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒 $$
数据集和超平面的距离
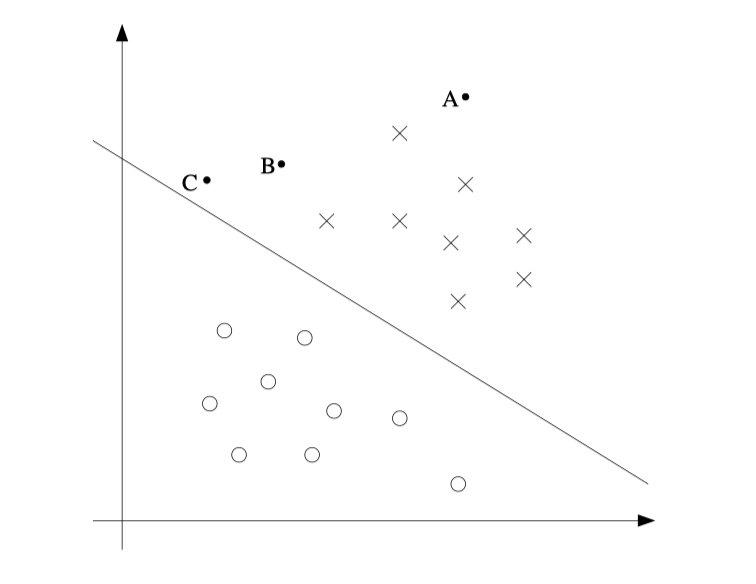
添加图片注释,不超过 140 字(可选)
定义边缘(margin)
geo- margin
从单个实例来看,就是向量到一个平面的距离,根据向量的推导知识可以看出: $$ geo_{margin}^{i}=y^{(i)}*(\omega^TX^i+b) $$ 从整个数据集来看,就是一群点到一个平面中距离的最小值,定义为 $$ geo_{margin}=min_{i=1}^m geo_{margin}^i $$
fun- margin
上述的几何边缘的定义中,最终出现的结果可能会出现结果会随着不同的w的取值而出现不同的情况,因此需要从归一化的角度来更新边缘 $$ fun_{margin}^{(i)}=\frac{y^{(i)}*(\omega^TX^{(i)}+b)}{||w||} $$ 同样定义数据集的fun margin $$ fun_{margin}=min_{i=1}^m\ fun_{margin}^{i} $$
得到模型(model)
最直观的,我们希望所有点的margin可以都以大于零,在这个约束的基础上,数据集的margin可以越大越好 $$ target:max[min_{i=1}^m y^{(i)}(\omega^TX^i+b)]\ s.t.:y^{(i)}(\omega^TX^i+b)>=0\ ||w||=1 $$ 在上述直觉的基础上,需要对模型进行进一步的调整
- 我们希望所有的margin都可以大于零,也可以说是希望所有的margin都大于最小margin(目标函数)的值 $$ max\ \hat\gamma\ s.t.:y^{(i)}(w^Tx^{(i)}+b)>=\hat\gamma\ ||w||=1 $$
- 可以将||w||=1的假设调整到目标函数上 $$ max\ \hat\gamma/||w||\ s.t.:y^{(i)}(w^Tx^{(i)}+b)>=\hat\gamma $$
- 同样的跟进一步,我们假设之间的距离为1 $$ \hat \gamma=1 $$ 那么模型等价于 $$ max\ \frac{1}{||w||}\ s.t.:y^{(i)}(w^Tx^{(i)}+b)>=\hat\gamma $$ 为了方便后续计算 $$ min \frac{1}{2}||w||^2 $$
- 由此转换为一个凸优化问题 $$ min \frac{1}{2}||w||^2\ s.t.:1-y^{(i)}(w^Tx^{(i)}+b)<=0 $$
0x03 求解模型
数学基础1(凸优化)
优化问题可以分为三类:
同样所有的优化问题,都可以转换成为对偶问题,来简化求解过程
- 无约束条件的优化问题 $$ min\ f(x)\ —\ eg:min\ f(x)=x_1^2+x_1-4 $$ 求解思路:求导完事了
- 仅含等式约束的优化问题 $$ min\ f(x)\ s.t.\ h_j(x)=0,j\in {1,2,…,n}\ —\ eg: min\ f(x)=2x_1^2+3x_2^2+7x_3^2\ s.t.\ 2x_1+x_2=1\ 2x_2+3x_3=2 $$ 求解思路:利用拉格朗日乘子法,见下一节
- 含不等式和等式的优化问题 $$ min\ f(x)\ s.t. h_j(x)=0,j\in {1,2,…,n}\ g_j(x)<=0,j\in{1,2,…,m}\
\ eg:min\ f(x)=x_1^2-2x_1+1+x_2^2+4x_2+4\ s.t.:x_1+10x_2>10\ 10x_1-x_2<10 $$ 求解思路:利用拉格朗日乘子法,但是需要满足KKT条件
数学基础2(拉格朗日乘子法)
求解上述:仅含等式约束的优化问题
首先构建拉格朗日函数 $$ L(x,\alpha)=2x_1^2+3x_2^2+7x_3^2+\alpha_1*(2x_1+x_2-1)+\alpha_2*(2x_2+3x_3-2) $$ 此时针对拉格朗日函数对变量X求导,希望等于0 $$ \frac{\partial L}{\partial x_1}=0\ \frac{\partial L}{\partial x_2}=0\ \frac{\partial L}{\partial x_3}=0 $$ 得到 $$ x_1=-\frac {1}{2}\alpha_1\ x_2=-\frac {1}{6}\alpha_1-\frac {1}{3}\alpha_2\ x_3=-\frac {3}{14}\alpha_2\ $$ 带入约束条件中求解等式,得到最优解
同样的求解上述:含有等式和不等式的优化问题
$$ L(x,\alpha)=x_1^2-2x_1+1+x_2^2+4x_2+4+\alpha_1(-x_1-10x_2+10)+\alpha_2(10x_1-x_2-10)\ \alpha_i>=0 $$
和上述相似对拉格朗日求导,希望等于0 $$ \frac{\partial L}{\partial x_1}=0\ \frac{\partial L}{\partial x_2}=0\ $$ 这里需要满足KKT条件 $$ 导数等于0* h(X)=0\ \Sigma_{j=1}^m\alpha_ig_i(X)=0 $$
数学基础3(对偶求解)
Slater条件:一个凸优化问题如果存在一个候选x是的所有不等式约束都严格满足,则存在是原问题的对偶问题的最优解
这样有时候可以简化操作计算,
求解SVM的凸优化问题
- 首先将优化问题转换成为一个 convex optimization(P)
- 因为满足Slater条件,P为对偶问题D是同解的
拉格朗日乘子法-P问题的函数: $$ L(x,w,a)=\frac{1}{2}||w||^2+\Sigma_{i=1}^na_i(1-y^{(i)}(wx^{(i)}+b)) $$ 原问题: $$ p=min_{w,b}max_a L $$ 转换为对偶问题 $$ d=max_amin_{w,b}L $$ 这里是将第三种凸优化问题转换成为一个无约束的第一种凸优化问题 $$ \frac{\partial L}{\partial w}=w-\Sigma_{i=1}^na_iy^{(i)}x_i^T=0\ \frac{\partial L}{\partial b}=\Sigma_{i=1}^na_iy^{(i)}=0 $$ 带入到拉格朗日函数中 $$ L=\frac{1}{2}\Sigma_{i,j=1}^na_ia_jy_iy_jx_i^Tx_j-\Sigma_{i,j=1}^na_ia_jy_iy_jx_i^Tx_j-b\Sigma_{i=1}^na_iy^{(i)}+\Sigma_{i=1}^na_i\ =\Sigma_{i=1}^na_i-\frac{1}{2}\Sigma_{i,j=1}^na_ia_jy_iy_jx_i^Tx_j $$ 约束条件: $$ s.t.:\Sigma_{i=1}^ma_iy_i=0\ a_i>=0 $$ 之后利用SMO算法来求解得到 $$ a_i $$ 之后得到hyperplane为: $$ \Sigma (a_iy^{(i)}x_i^Tx_j+b) $$
0x04 分类讨论
- 在线性可分的情况下可以顺利的求解出 a_i
- 加入松弛变量和惩罚因子来找到相对更好的hyperplane
- 使用kernel trick来将低维映射到高纬的空间,使得在高纬空间中数据是线性可分的
详细介绍kernel trick:
本来是在低维中直接内积 $$ x_i^Tx_j $$ 之后希望都从地维转换到高纬,在计算内积 $$ \phi(x_i)^T\phi(x_j) $$ 跟进一步,希望直接在低维空间计算高维内积 $$ 线性核:x_i^Tx_j\ 多项式核:(x_i^Tx_j+1)^q\ 高斯核:exp(-\frac{(||x_i-x_j||^2))}{2}\ sigmoid:tanh(x_i^Tx_j+1) $$
0x05 SVM code
借鉴别人的,留一个坑自己写
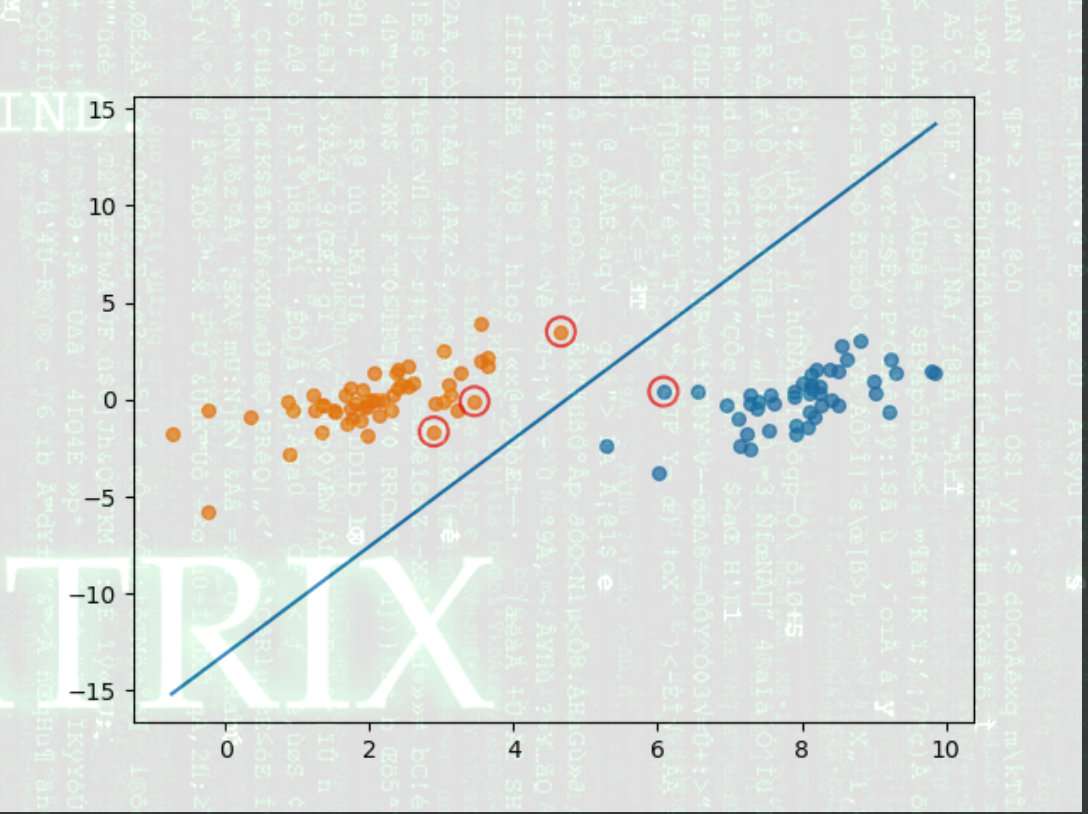
添加图片注释,不超过 140 字(可选)
1 | |
/datasets/testSet.txt
1 | |