CS229机器学习 boosting 方法 | Vol10
对决策树中有关的boosting方法进行总结,包括最基本的Adaboost、然后了解从提升树(Boosting Tree)到之后的梯度提升回归树(Gradient boosting decision tree),希望可以了解其中的Boosting方法的脉络,也为之后的XGBoost和LightGBM的学习奠定基础
0x01 背景知识
1.1 决策树(Decision tree)
决策树是一种基本的机器学习模型,具有分类和回归的功能。它的特点是具有分类速度快,模型容易可视化的解释,缺点是容易发生过拟合
决策可以分为分类树和回归树

添加图片注释,不超过 140 字(可选)
1.2 集成学习 (Ensemble learning)
为了将弱学习器(Weak learner)集中其中形成这个具有多学习器综合的条件,我们可以采用不同的算法和数据集融合的方式来构建模型、也可以采用不同的融合方法比如平均法投票法stacking、或者采用特殊的技巧比如bagging和boosting的方式
其中XGboost和GD都属于boosting的方法范畴,其工作原理是初始训练集训练得到一个基学习器,再根据基学习器的表现对训练样本分布进行调整,使得之前基学习器出错的训练样本后续可以得到更多的关注,然后基于调整后的样本分布来重新训练学习器,最终继承多个学习器并根据错误进行加权来得到最终的学习器
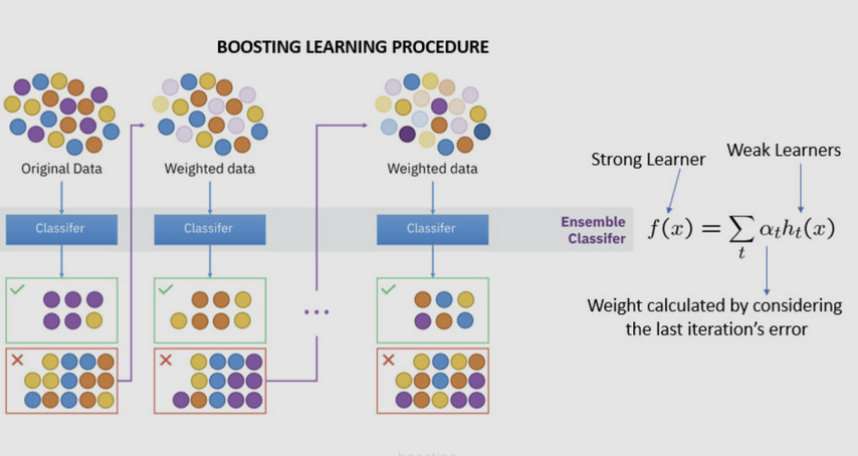
添加图片注释,不超过 140 字(可选)
1.3 回顾机器学习
机器学习从组成部分中最重要可以说分为四个部分
- 数据集(dataset)
- 模型(model)和参数(parameters)
- 目标函数(objective)= 损失(loss)+正则化(regularization)
- 优化方法(optimization method)
0x02 AdaBoost算法
2.1 简介
每次学习之后,迭代更新样本数据集中的权重来重新生成一颗决策树,之后根据准确率来组合所有的学习器实例得到最终的结果
2.2 算法过程
给定一个二分类的数据集$T={(x_i,y_i)}_{i=1}^{i=N}$,X是特征集合,y是标记集合。
算法的流程(AdaBoost) 输出为G(X)
1-1 首先,初始化训练数据中的权重分布,最初都相同权重
之后训练M颗树,对于M=1,2,…,M
2-1 根据权重分布$D_m$训练数据集来得到基本分类器
《李航统计学习》没有提到的部分就是如何根据权重来重新计算分类器;个人推测是在决策树分类的过程中,对不同类别的比例按照权重来重新计算,比如均匀分布的时候1和-1的比例为6:4;如果有权重需要根据对其中错误的类别进行分类:(30.07+30.16):4*0.07
2-2 计算得到的分类器在训练数据集中的误差率
2-3 由此来得到分类器对应的权重
2-4 在进行下一步计算的过程中,更新下一次的训练的权重,$Z_m$的作用是为来归一化
3-1 这样反复迭代得到基本分类器的线性组合
G(x)就是最终的输出,有时候为了防止过拟合,也可以使用学习率来控制$f(x)$的增加速度
2.3 AdaBoost例子
见《李航统计学习131页》

添加图片注释,不超过 140 字(可选)
2.4 算法的分析和解释
关于AdaBoost的解释可以分为两种
- 是通过统计学习的理论来推到出AdaBoost的训练误差边界、和相关推广的定理
- 认为它是模型为集成策略为additive、损失函数为exp、学习算法为前向分布算法(forward Stagewise algorithm)
其实AdaBoost中一个问题就是权重的选取为什么是这个样子的?
这里我们可以结合前向分布来进行推导,这里的目标函数是
也正是因为这个限制,AdaBoost只能作为二分类来学习,
1-1 加法模型,就是我们可以
其中 $\alpha_m$为权重,$f_m(x)$是根据第M次训练得到的分类器,接下来就是确定这两者的取值,我们的目标是
由于在M次训练的时候,$G_{m-1}(X)$没有影响,所以可以分离开来作为比例项
根据加权数据来重新训练得到$f_m(X)$。
对于$\alpha_m$可根据求导得到答案
注意这里只是一个二分类的问题,所以化简之后得到的答案
2.5 优缺点
优点:
分类精度高,可以用各种回归分类模型作为构建学习,非常灵活,不容易过拟合
缺点:
对于异常值敏感,会获得较高的权重
0x03 梯度提升简介 Gradient Boosting
3.0 直觉background
参考链接5,下文给出,写的非常好

添加图片注释,不超过 140 字(可选)
3.1 提升树 Boosting Tree
提升树是按照分类树或者回归树作为基本分类器的提升方法,提升树被认为是统计学习中性能最好的方法之一,针对不同问题的提升树的学习算法主要在于损失函数不同,包括平方误差损失函数、指数损失函数的分类问题和一般损失函数的一般决策问题
回归问题中的提升树算法
1-1 初始化模型
2-1 对于m=1,2,…,M不断迭代
2-2 计算上一个模型留下来的残差
2-3 重新计算一个回归树
2-4 更新现有的模型
2-5 得到最终的回归树
[gradient_boosting.pdf](https://zhuanlan.zhihu.com/Gradient Boosting算法的原理解析 adea61fa3573481aaf9534834231c2c8/gradient_boosting.pdf)
每一次建立模型是在之前建立模型损失函数的梯度下降方法,损失函数是评价模型性能,如果可以让损失函数可以持续下降,就能够使得模型可以不断改变提升性能,其中最好的方法是让损失函数可以沿着梯度的下降进行更新迭代
3.2 梯度提升 Gradient Boosting(for regression DT)
最开始GBDT只能解决回归问题,但是后续工业的调整之后允许分类
从上述我们可以看出对于分类和回归模型下来的思路,但是后续我们应该怎么办?对于其他类型的损失函数,我们如何去训练整个过程,这个时候就需要利用梯度下降(Gradient decent的思路)
残差其实是根据很直觉的想法来得到的,但是对于更加复杂的损失函数比如交叉熵之类的,简单的残差是没有意义的,所以为了保证整个算法可以走下去,使用梯度下降的方法
在其中使用shrinkage的方法,来保证每次仅仅改变一丝,来逐渐的得到梯度提升回归树
可以看出梯度提升(Gradient Boosting)和AdaBoost之间的细微的区别在于:对于错误的数据,AdaBoost采用改变其样本分布的权重增大比例,而梯度提升是利用残差的大小来提高错误数据在模型中的重要性
reference:
《统计学习方法》-李航
《机器学习》-周志华
https://blog.csdn.net/shine19930820/article/details/65633436
https://www.ccs.neu.edu/home/vip/teach/MLcourse/4_boosting/slides/gradient_boosting.pdf
[https://blog.csdn.net/shine19930820/article/details/65633436](