CS229机器学习 实验设计 | Vol5
非常喜欢《机器学习导论》中关于感知器的一句话:“神经网络的目的不是为了研究人脑的内部结构和运行机理,而仅仅是模仿来作为一个学习罢了”,通过这句话可以看出机器学习作为一门工程类的学科,本质目的还是为了寻找一种好的方法,在此过程中就要思考需要用什么样的标准来评价好坏?这是一个曾经观察高中物理、高中化学、高中生物中的实验科学,更进一步,我们更有着统计的知识来指导我们更近一步地正确设计实验。
0x01 引言
机器学习中,实现一个目标中可以有很多中不同的学习算法,来么:
- 如何评估一个学习算法在给定问题上的期望误差?
- 对于同一个目标的不同学习算法,我们如何证明一个算法比另外一个算法误差更低?
我们不能只看训练集上的误差来作为判断,因为具有更复杂度的模型的误差总是比简单模型小
同样在不同与训练及的验证集中一轮运行也不够,因为可能会有噪声和离群点的影响,同样具有超参数的算法的泛化过程中会有这其他的随机因素。我们通过运行learning algorithm来得到一个leaner;如果我们只训练一次只得到一个leaner和一个validation error,为了平均各种随机性,我们需要产生多种leaner,进而在多个验证集上评估,我们对learning algorithm的评估是应该是基于这些validation error的distribution来的,通过评估expected error或者是variance来进行比较。
总结上述,可以看出我们的目标是规划和设计机器学习实验,来分析实验产生的数据,以便能够排除随机性的影响,得到统计显著的结论,在机器学习中,我们的目标是得到具有最高的泛化准确率、最小复杂度的学习器,并且该学习器是robust
我们在实验设计中需要设计的3项基本原则:
- randomization随机化,要求实验运行的次序应该是随机确定的,这样使得结果是独立的
- replication重复,因为这应该对可控因素的相同配置多次实验,以便平均不可控因素的影响,通常在相同数据集上再抽样的版本上叫做交叉验证(cross- validation)
- blocking阻止,用来降低或消除有害因素导致的可变性,准确率的差异不仅取决于不同的算法还取决于不同的子集,因此为了度量仅由算法导致的差别,重复运行的不同训练集应该是相同的,在统计中常有配对检验(pairing test)
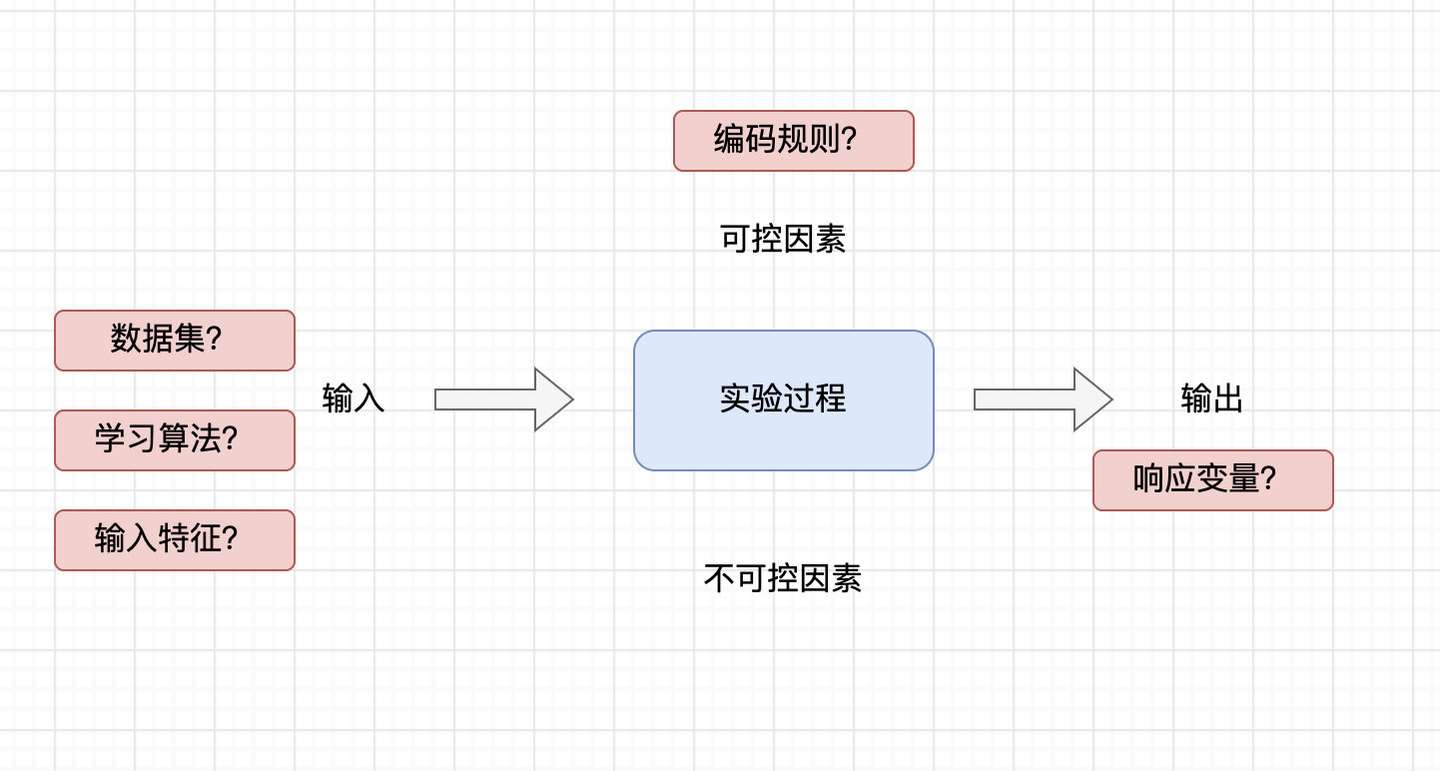
添加图片注释,不超过 140 字(可选)
0x02 实验设计的基本策略 strategy of experimentation
这里感觉更多是关于如何调参的选择,如何设计对比出不同算法优劣,比如消融实验之类的还是依靠实践
最佳猜测 best- guess
从某个我们相信是好配置的因素设置开始,在此检验响应之前,每次稍微改动一个或者少量因素,来检验每个组合指导得到一个足够好的状态
一次一个因素 one factor at a tiem
我们为每个因素确定一个基线的抹额认知,然后对一个因素尝试不同水平而令其他因素保持在极限上,这种方法的缺点是假设因素之间不相互影响
因素设计 factorial design
通常也被称为网格搜索grid search,其中因素一起变化而不是单因素变化
响应面设计 response surface design
通过设计合理的有限次数试验,建立一个包括各显著因素的一次项、平方项和任何两个因素之间的一级交互作用项的数学模型,精确研究各因素与响应值之间的关系,快速确定多因素系统的最佳条件,常用具体方法有:中心复合试验设计(central composite design CCD)和Box-Behnken试验设计(DDB)
0x03 模型选择–重复样本
hold-out 通常对获得数据集之后,会将其划分出来一部分不会使用的test set;在训练过程中的会用到的有train set和validation set
通常train set和validation set之间的比例可以为10或者30,但是不幸的是样本通常没有这么多,因此我们应该在小数据集上尽力而为,其方法是以不同划分来重复使用它,这种称为交叉验证cross- validation,但是潜在的问题有交叉验证使得错误率是相互依赖的,因为这些不同集合共享数据
在重复爱漾中要尽可能的保持分层stratification,我们希望保证误差估计的鲁棒性,同时要保持不同集合间的重叠尽可能的小,还不能扰乱类的先验概率
3.1 K- fold CV
将训练的书籍划分为K等分,将K份数据集中的一份划分为验证集,其他作为验证集,在较为极端的医疗中可能会有leave-one-out
3.2 5x2 CV
很神奇而让人不想去了解
3.3 bootstrapping(自助法)
采用从原始样本中以有放回地抽取实例的方法来产生新的样本,自助样本可能比交叉验证有更多的重叠,因而其估计可能更相互依赖 $$ (1-\frac{1}{N})^N=1/e=0.368 $$ 意味训练集中包含63.2%的实例,将原始数据集作为验证集
0x04 模型选择–性能度量
4.1 分类
二分类的混淆矩阵confusion matrix
| | 预测positive | 预测negative | | | ———— | ———— | ———— | —- | | 正例positive | TP | FN | | | 负例negative | FP | TN | |
$$ 误差:(FP+FN)/N\ 准确率:(TP+TN)/N\ 精度:TP/(TP+FP)\ 召回率:TP/(TP+FN)\ 灵敏度:召回率\ 特效性:TN/fp+tn\ tp-rate:tp/p\ fp-rate=fp/(tn+fp) $$
关于假正和假负,例如一个用户希望登陆另外一个用户的账户,假正是允许顶替,假负是正常用户登陆不了,显然前者危害会更高 tp-rate:衡量通过身份认证合法用户的比例 FP-rate:错误接受顶替的比例
(tp-rate,fp-rate)得到ROC(receiver operating characteristic),该曲线下面的(area under the curve AUC)可以来比较不同损失条件下平均的整体性能
可以参考科技文献检索中的查全率和查准率
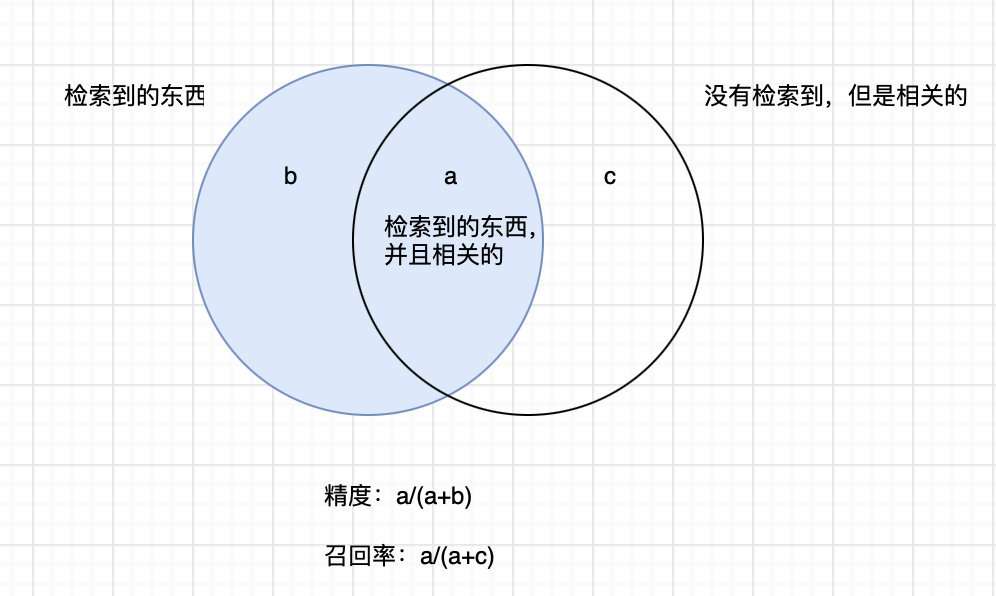
添加图片注释,不超过 140 字(可选)
class confusion matrix
4.2 回归
mean square error
RMSE之类的
0x05 模型选择 – 结果可靠性(看不懂,统计功底不够)
5.1 区间估计 interval estimation
《概率论》
5.2 假设检验 hypothesis testing
《概率论和数理统计》
5.3 结合评估性能
一下用于对分类问题中的错误率进行分析,同样可以适用于回归的就放误差、非监督学习的对数似然、增强学习的期望奖励等
单个学习器的错误率衡量
二项检验
近似正态检验
t检验(K-fold)
比较两个分类算法错误率
McNemar检验
K折+t检验