数据结构和算法设计 Vol2

这里主要借鉴Tsinghua的2020fall<数据结构与算法>这本书，包含对于一些基本数据结构的探索，先从定义梳理，在整理题目，之后是实际训练。结合之前在程序设计或嵌入式中对于数据在实际存储的例子来学习可能会更好。从中也能体悟到算法一些含义

本次主要对图（Graph）的基本知识点，和一些实际应用的算法进行描述，但是在另外一方面，图也不仅仅存在于数据结构中，在运筹学中对图也有相关的描述，因此希望在这里整合两者之间的概念，并分别介绍两者的应用，挺有意思的。

0x01 数据结构中的图 Graph

例如之前例子中的迷宫，借助绳索掌握迷宫内各通道之间的相互关系，在很多应用中我们需要准确有效描述和利用这类信息，这类信息往往可以表述为定义与一组对象之间的二元关系，比如城市交通图、比如互联网中的IP地址，尽管上一章的树 Tree结构也可以用来表示这种二元关系，但是仅限与Parent Node 和Child Node之间，这种一般性的二元关系属于图论 Graph Theory的范畴

本章的主要目的

简要介绍图（Graph）的基本概念和术语
如何实现作为抽象数据类型（ADT）的图结构，主要讨论邻接矩阵（Adjacent matrix），和邻接表（Adjacent list）两种实现方式
从遍历（traverse）的角度介绍将图（Graph）转换为树（Tree）的典型方法，包括广度优先搜索（BFS）和深度优先搜索（DFS）
分别以拓扑排序和双连通域分解为例子，介绍利用基本数据结构并基于遍历模式，设计图算法的主要方法
（数据结构决定遍历次序）的观点出发，将遍历算法概括并统一为最佳优先遍历这一模式，如此来更加准确和深刻理解不同图算法之间的共性与联系，更可以学会通过选择和改进数据结构，高效设计并实现各种图算法

1.1 概述

图（Graph）定义为G=（V，E）。集合V中的元素为顶点（Vertex），集合E中的元素分别对应于V总的某一对顶点（u,v），表示它们之间存在的某种关系，因此可以称为边（Edge），从计算需求的角度约定都是有限集，规模分别记为n和e

无向图（undirected graph），若边(u,v)所对应顶点的u和v的次序无所谓，称作无向边（undirect edge）；
有向图（directed graph）。如果不对等，称为directed edge，如果从u指向v，则其中u是该边的origin或者尾顶点tail，v是该边的终点destination或头顶点head
如果包含有向边和无向边，可以称为混合图mixed graph

添加图片注释，不超过 140 字（可选）

度（Degree），对于任何一边e=，可以称顶点u和v彼此邻接（adjacent），同时与边e彼此关联（incident）。在无向图中，与顶点v关联的边数称为v的度数（degree），记deg（v）；在有向图中，出边总数称为出度（out-degree）、入边总数称为（in-degree）

简单图（Simple Graph），指的是不包含任何自环的图（Self-loop），自环指的是联接与同一顶点之间的边，在某些场景中具有特定意义，但在简单图中不讨论。

通路（path）就是由m+1个顶点于m条边交替而成的一个序列，也就是说这些边依次首尾相连，其中沿途的边的总数m是通路的长度。注意通路中的边必须互异，但是顶点可能重复，当顶点都不相同称为简单通路（Simple path）

环路（cycle）就是在通路的基础上加上起止顶点相同，对于不包含任何环路的有向图称为有向无环图（directed acrylic graph，DAG），如果环路中除了起点和终点的顶点相同，其他都是一样的称为简单环路（Simple cycle）。一些特殊的环路，欧拉环路（Eulerian tour）是图中各边一次且恰好一次的环路；对偶的，哈密尔顿环路（Hamiltonian tour）是经过图中各顶点一次且恰好一次的环路

添加图片注释，不超过 140 字（可选）

带权网络（weighted network，G（V，E，wt（）））需要通过一个权值函数，为每一边e指定一个权重weight，wt（e）指定边e的权重

复杂度（complexity），在这个过程中n各顶点，最多有e=O（n^2)来进行描述

1.2 抽象数据类型的实现

也就是图（Graph）操作的一些方法，一般常见的实际方法，具体实现过程略过（看不懂，暂时觉得没必要）

添加图片注释，不超过 140 字（可选）

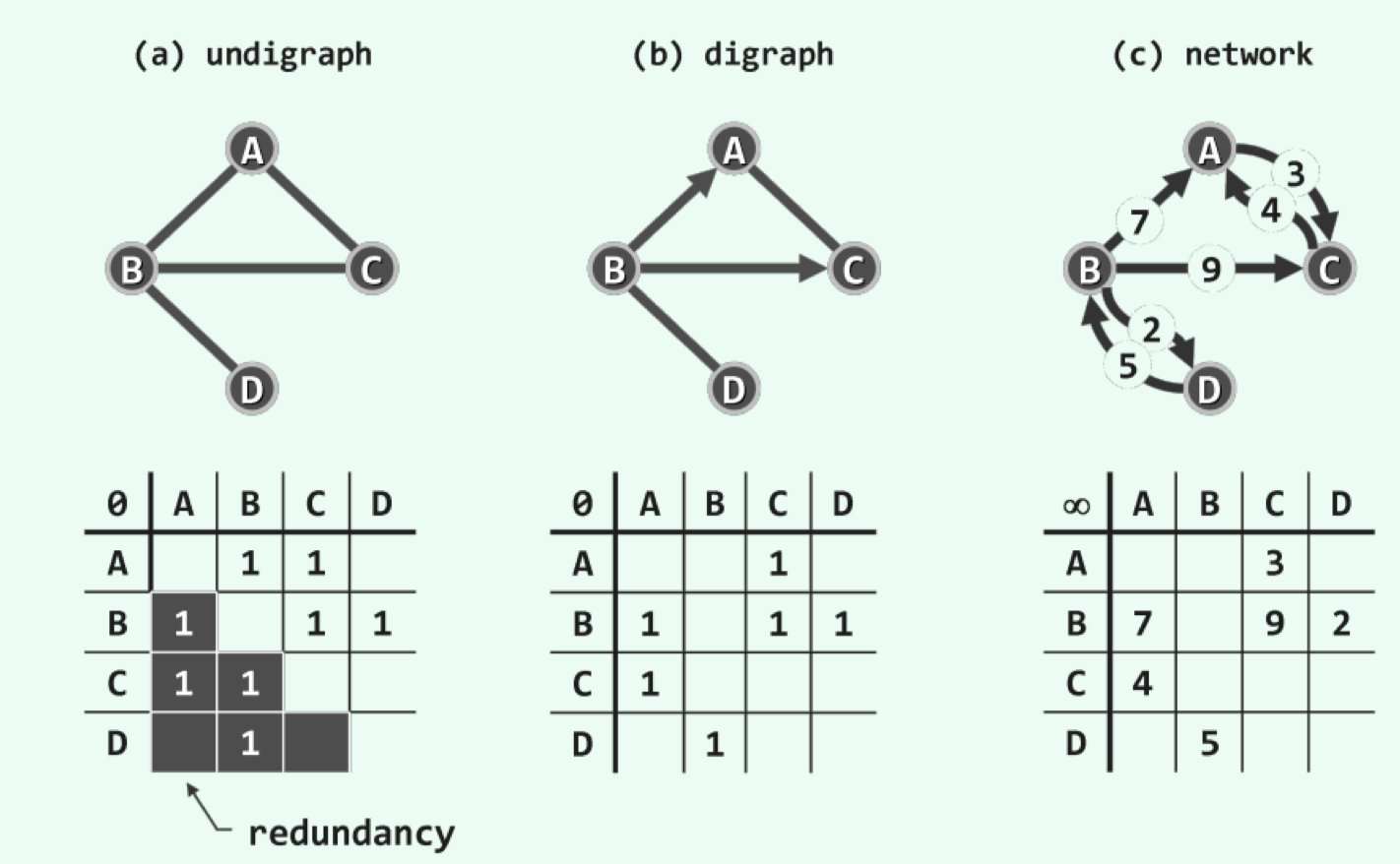
1.3 邻接矩阵 Adjacent matrix

邻接矩阵是图（Graph）的ADT（Abstract Data Type），使用方阵A[n][n] 表示由n顶点构成的图，其中的每个单元负责描述顶点之间可能存在的邻接（Adjacent）关系

对于无权图，存在和不存在使用0-1来表示

对于带权网络，此时可以将矩阵中各单元从bool转换为int或者float类型，对于不存在的边使用0或者∞来代替

添加图片注释，不超过 140 字（可选）

代码实现过程略过

1.3.1 时间性能

各顶点编号可以直接转换为其Adjacent matrix中对应的Rank，从而使得ADT中所有的静态操作接口的时间只需要O（1）时间

另外边的静态和动态操作只需要O（1）的时间，代价是Adjacent matrix的空间冗余

但是这种方法并非完美无缺，不足点在于顶点的动态操作接口十分耗费时间，为来插入新的顶点，V[]中需要添加一个元素，同时边集向量E[][]也需要增加一行，且每行都需要添加一个元素，顶点的删除操作也是类似；在通常的算法中顶点的动态操作远少于其他操作，而且计入向量扩容的代价，单次操作的耗时不过O（n）

1.3.2 空间性能

对于无向图而言，邻接矩阵必须为对称阵，其中除自环以外的每条边都被重复存放来两次，因此有一半的单元都是冗余的，也就是O（n^2）

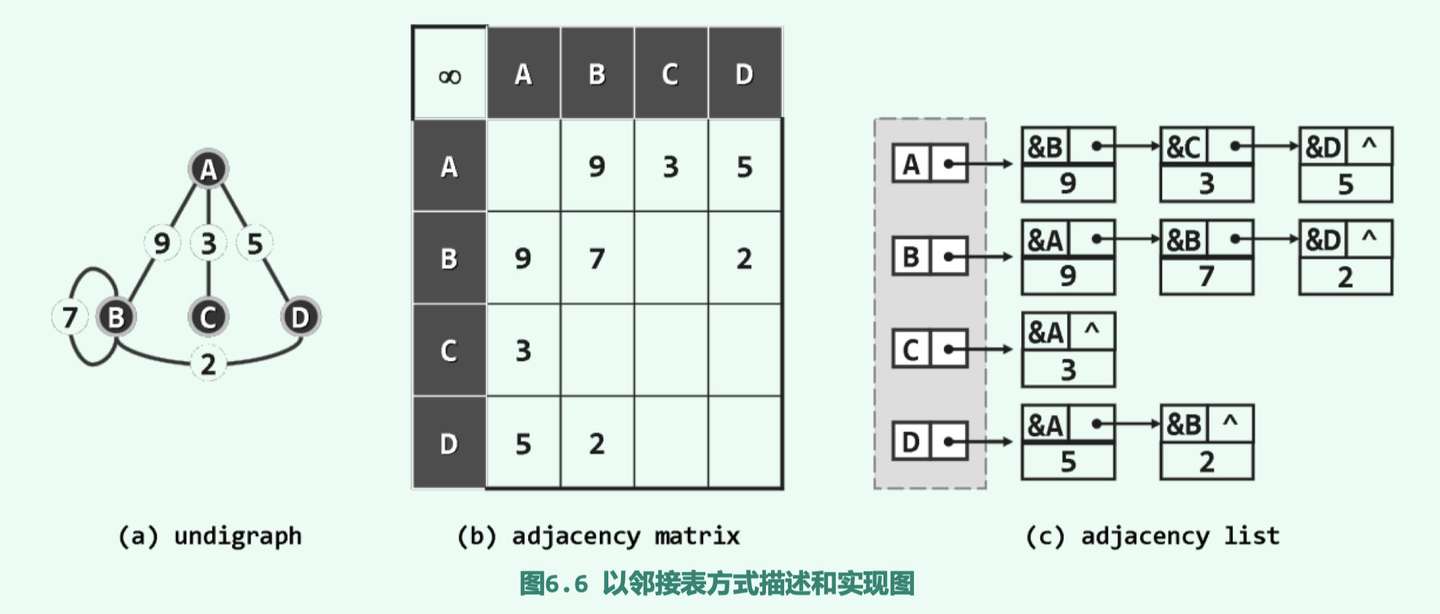
1.4 邻接表（adjacent list）

在上述邻接矩阵（Adjacent matrix）的空间解释中可以看出其空间的仍存在改进的余地，在实际应用中处理的图所含有的边通常远远少于O（n^2)，比如在平面图之类的稀疏图（sparse graph）中，边数渐进不超过O（n），仅仅与顶点总数大致相当

为了完善这种静态空间管理策略所导致的问题，因此可以使用图结构的另外一种表示与实现方式，可以将邻接矩阵转换称邻接表的方式，分别记录每个顶点的关联边（或者等价的邻接顶点）来构成邻接表（adjacent list）

添加图片注释，不超过 140 字（可选）

1.4.1 时间复杂度分析

复杂度分析，adjacent list中的列表等于顶点总数N，每条边在其中仅存放一次（for direct graph）或者两次（for undirected graph），因此空间总量为O(n+e),与图自身的规模相当，相比较adjacent matrix有很大的改进

在空间性能的改进，相对应的是时间性能的降低为代价，比如判断顶点v与顶点u的边是否存在，需要O(n)时间

与顶点相关的动态操作，顶点的插入操作可以在O（1）的时间内完成，顶点的删除操作需要遍历所有的adjacent list，需要O（e）时间

1.4.2 空间复杂度分析

adjacent list在访问单条边的效率并不算高，但是适合用循环的额方式，处理同一顶点的所有关联边比如为了枚举从顶点v出发的所有边，仅需要theta(1+outdegreee(v))而不是theta(n)的时间

1.5 图（Graph）遍历算法概述–BFS和DFS

图算法中大部分成员的主体框架都归结于图的遍历，与树的遍历相似，图的遍历需要访问所有顶点一次且仅有一次，此外图遍历同时还需要访问所有的边一次且仅一次

同时无论采用何种策略和算法，图遍历都可以理解为将非线性结转化为半线性结构的过程，经遍历而确定的边类型中，最重要的一类就是所谓的树边，它们与所有顶点共同构成来原图的一颗支撑树，称为遍历树traversal tree

图中顶点之间可能存在多条通路，为来避免对顶点重复访问，在遍历的过程中，通常还需要动态设置不同顶点的状态，并随着遍历的进程不断转换状态，直至最后的“访问完毕”，图的遍历更加强调对处于特定状态顶点的甄别与查找，因此也称为图搜索（Graph search）

深度优先搜索、广度优先搜索、最佳优先等基本而典型的图搜索，都可以在线性时间内完成，也就睡这些算法仅需要O（n+e）的时间来访问所有的顶点和边

各种图搜索之间的区别体现在边分类结果的不同，以及所得遍历树的结构差异，其决定因素在于搜索过程的每一步迭代，将依照何种策略来选取下一接受访问的顶点

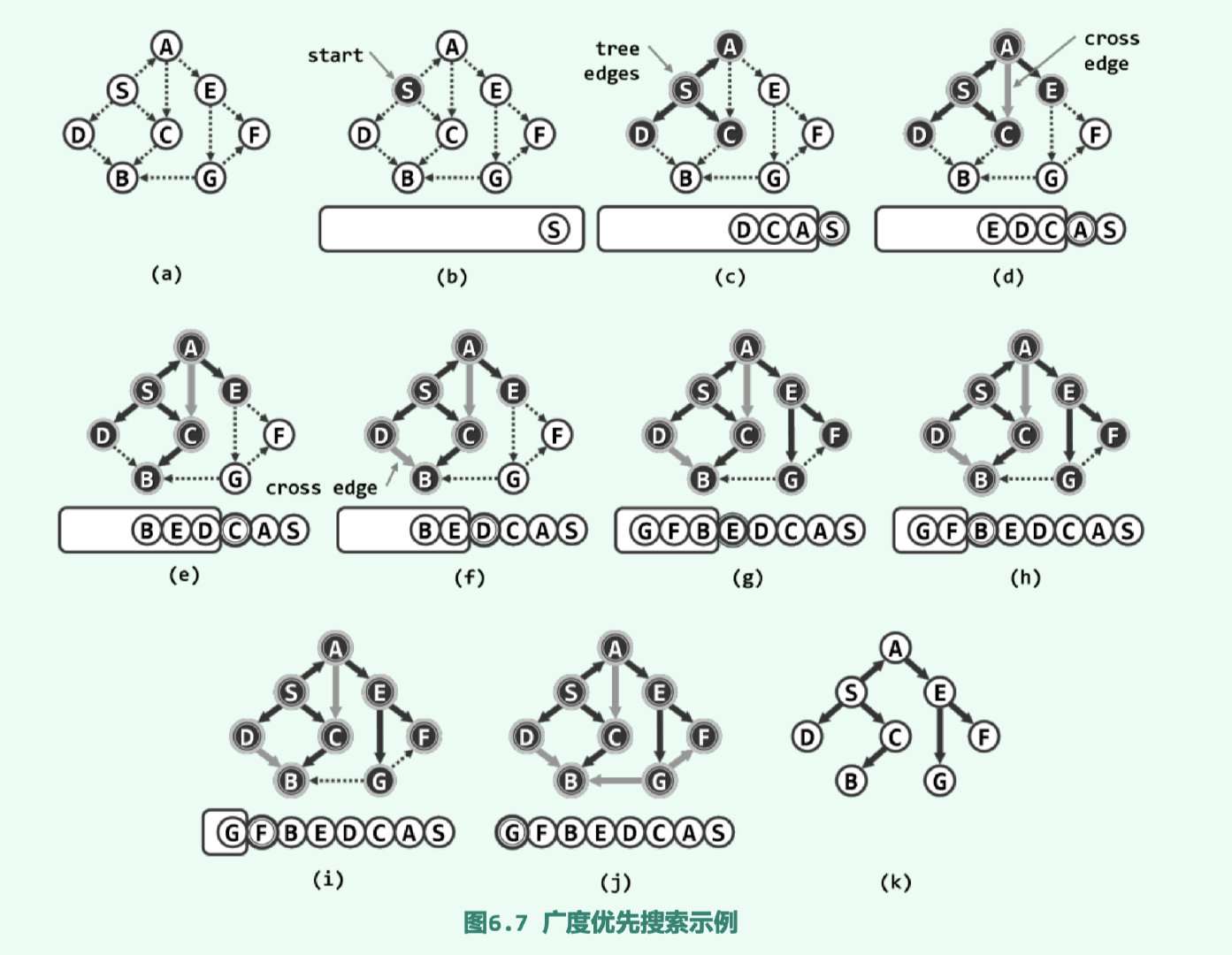
1.5.1 广度优先搜索 breadth-first-search BFS 越早被访问到的顶点，其邻居被优先选用

搜索的过程：反复从前沿集（frontier）中找到最早被访问到顶点v，若其邻居均已访问到，则将其逐出前沿集，否则随意选出一个尚未访问到的邻居，并将其加入到前沿集（frontier）

添加图片注释，不超过 140 字（可选）

由于每一步迭代都有一个顶点被访问，因此最多迭代O（n），另一方面因为不会泄漏每个刚被访问顶点的任何邻居，因此对应无向图（undirected graph）必能覆盖s所属的连通分量（connected component），对于有向图必能覆盖以s为起点的可达分量（reachable component）

// 图的广度优先搜索算法
void Graph::bfs(int s){ //assert 0,n
reset();
int clock=0;
int v=s; //初始化
do
    if (UNDISCOVERED == status(v))// 一旦遇到尚未发现的顶点
        BFS(v,clock);
while (s !=(v=(++v %n))// 按照序号检查

void Graph::BFS(int v, int& clock){
    Queue Q;//辅助队列
    status(V)=DISCOVERED;
    Q.enqueue(v);//初始化起点
    while(!Q.empty()){
        int v=Q.dequeue();
        dTime(v)=++clock;//取出队首顶点v
        for(u=firstNbr(v);-1<u;u=nextNbr(v,u))
            if(status(u)==UNDISCOVERED){
                status(u)=DSICOVERED;
                Q.enqueue(u);//发现顶点
                type(v,u)=TREE;
                parent(u)=v;
            }else
                type(v,u)=CROSS;
    }
    status(v)=VISITED
}

}

### 1.5.2 深度优先搜索 depth-first-search，DFS 优先选取最后一个被访问到的顶点的邻居

以顶点s为基点的DFS搜索，首先访问顶点s，再从s所有尚未访问到的邻居中任取其一，并以之为基点，递归地执行DFS搜索，故各顶点被访问到的次序，类似与树的先序遍历，而各顶点被访问完毕的次序，则类似于树的后序遍历

添加图片注释，不超过 140 字（可选）

0x02 交通运筹学中的图

2.1 交通中图的例子

轨道交通中的图

添加图片注释，不超过 140 字（可选）

18世纪哥尼斯堡城的，普雷格尔的两岸和河中两个岛之前有七座桥

添加图片注释，不超过 140 字（可选）

经典的收发问题

2.2 基本概念–无向图G

无向图，设 V 是一个有n顶点的非空集合：V={v1，v2，v3，…，vn}；E是一个有m条无向边的集合：E={e1，e2，..，em}，则称V和E这两个集合组合一个无向图，记做G=（V，E）

基于无向图的G的结构特点，给出下列术语

平行边，如果两条不同的边具有相同的端点，称为e和e‘是G的平行边
简单图，如果图G中没有平行边则为简单图（！！有点不一样）
完备图，若图G中任何两个顶点之间恰好有一条边相关联，则称图G是完备图
子图，G1=（V1，E1）并且V1属于V、E1属于E
生成子图，G1是G的子图，并且V1=V，则称G1是G的生成子图
导出子图，若非空E1属于E，则E1及包含的顶点时G的导出子图
链，无向图中一个由顶点和边交替而成的非空有限序列，Q=v0e0v1e1v2，如果起始点相同是闭链，不想等位开链
初等链，若开链Q中诸顶点都不相同，则称Q为一条初等链
回路，若一个闭链除链第一个顶点和最后一个顶点相同之外，没有其他相同的顶点和相同的边则称为回路
连通图，若图G中任意两顶点u和v之间存在一条链，则称为图G为连通图。否则被称为分离图
割边，若G为连通图，将G中边e取走后所得图为分离图，则称e为图G的割边

2.3 基本概念–有向图D

有向图，设 V 是一个有n顶点的非空集合：V={v1，v2，v3，…，vn}；E是一个有m条有向边的集合：E={e1，e2，..，em}，则称V和E这两个集合组合一个有向图，记做D=（V，E）

类似的有向图D也有术语

平行边，不同有向边的e与e‘的起点与终点相同
孤立点，V中不与E任一条边关联的点称为D的孤立点
简单图，无平行边的称为简单图
完备图，图中任何两个顶点，存在有向边（u，v）和（v，u），则该有向图D为完备图
基本图，将有向图D的每条边除定向就得到一个相应的无向图G，则G位D的基本图
子图，同上
导出子图，同上
导出生成子图，同上
同构图，如下图，顶点和边是相等的，由于同构图被认为是相同的，这就给我们在网络规划中建立网络模型带来许多方便，当我们使用几何图来构建网络模型时，点的位置可以任意布置。边的长短曲直可以任意，因此需要尽量设计这种反应问题清晰、简练的几何图

添加图片注释，不超过 140 字（可选）

链，若Q是有向图D的基本图G中的一条链，则Q为D的一条链
初等链，若Q是有向图D的基本图G的一条初等链，则Q被称为D的一条初等链
路，若Q是有向图D的基本图G中一条链
路径
回路，第一个顶点和最后一个顶点相同

2.4 基本概念–矩阵表示

关联矩阵，行表示顶点，列表示边，使用1表示是否链接

添加图片注释，不超过 140 字（可选）

邻接矩阵，行表示顶点，列表示顶点，使用数目表示两个顶点之间的链接数量

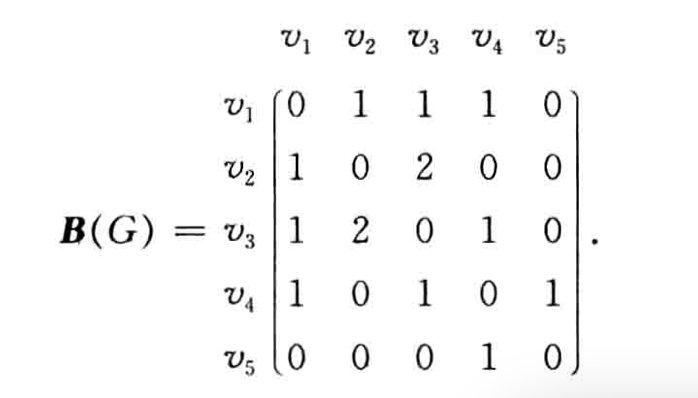
添加图片注释，不超过 140 字（可选）

2.5 树

不做赘述

0x03 数据结构中图的应用

3.1 拓扑排序（topological sorting）

以教材的编写实际问题为例子，作者可以借助有向图的结构整理出相关知识点之间的依赖关系，因向量是散列表和查找表的基础知识点，等等得到一份有向图，在这个基础上如何将这个有向图（undirected graph）来得到具有前端的顺序的额拓扑排序（topological sorting）

相容：每一个顶点都不会通过边，指向其在此序列中的前驱顶点，这样的一个线性序列，称作原图的拓扑序列

添加图片注释，不超过 140 字（可选）

针对有向无环图（directed noloop graph），问题在于topological sorting是否必然存在，如果存在是否唯一？

同理，有限偏序集中也必然存在极小元素（同样，未必唯一）。该元素作为顶点，出度必然为零比如图6.10(b)中的顶点D和F。而在对有向无环图的DFS搜索中，首先因访问完成而转换至VISITED状态的顶点m，也必然具有这一性质；反之亦然。

166

进一步地，根据DFS搜索的特性，顶点m（及其关联边）对此后的搜索过程将不起任何作用。于是，下一转换至VISITED状态的顶点可等效地理解为是，从图中剔除顶点m（及其关联边）之后的出度为零者在拓扑排序中，该顶点应为顶点m的前驱。由此可见，DFS搜索过程中各顶点被标记为VISITED的次序，恰好（按逆序）给出了原图的一个拓扑排序。

此外，DFS搜索善于检测环路的特性，恰好可以用来判别输入是否为有向无环图。具体地，搜索过程中一旦发现后向边，即可终止算法并报告“因非DAG而无法拓扑排序”。

3.2 双连通域分解

考查无向图G。若删除顶点v后G所包含的连通域增多，则v称作切割节点（cut vertex）或关节点（articulation point）。如图6.13中的C即是一个关节点它的删除将导致连通域增加两块。反之，不含任何关节点的图称作双连通图。任一无向图都可视作由若干个极大的双连通子图组合而成，这样的每一子图都称作原图的一个双连通域（bi-connected component）。例如图6.14(a)中的无向图，可分解为如图(b)所示的三个双连通域。

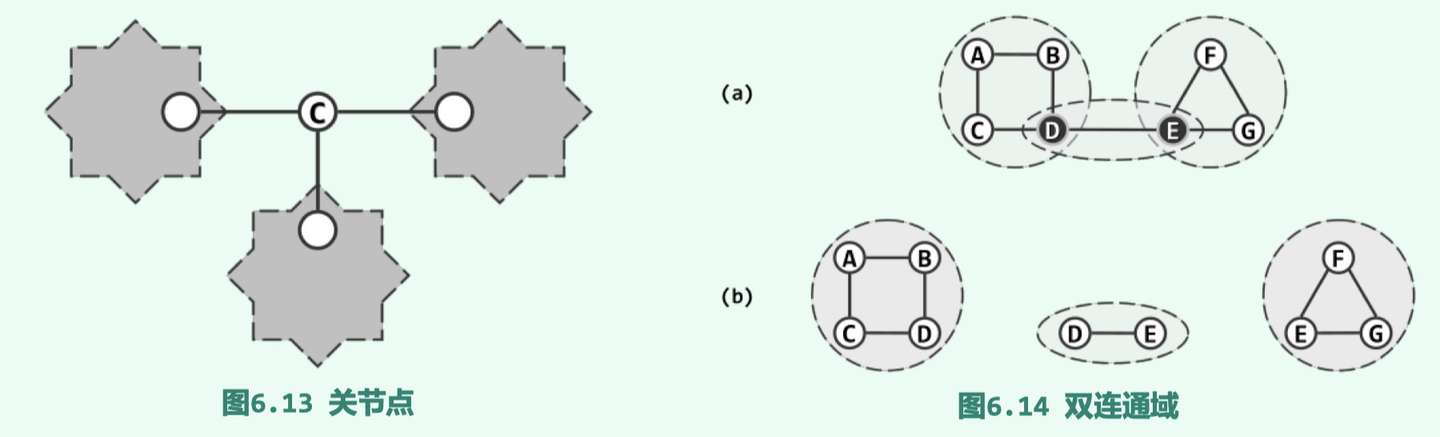
添加图片注释，不超过 140 字（可选）

3.3 优先级搜索

上面的图搜索应用虽然各有特点，但是其基本框架缺基本相似，总体而言都是通过迭代逐步发现各顶点，将其纳入遍历树中并做相应处理，同时根据应用问题的需求适当给出解答，各算法在功能上的差异，主要体现在每一步迭代中对新顶点的选取策略不同，比如BFS搜索会优先考察更早被发现的顶点，而DFS会更侧重于最后被发现的顶点

总结上述策略，可以看出其本质上是给所有顶点赋予不同的优先级，随着算法的推进不断调整，而每一步迭代所选取的顶点都是当时的优先级最高者，按照这样的理解，可以将BFS和DFS纳入统一的框架，称为PFS（priority-first search）

在实际应用中，引导优化方向的指标，往往对应于某种有限的资源或成本（比如通讯带宽、机票价格等）因此这里不妨约定优先级越大顶点的优先级越低

通过最小支撑树和最短路径这两个经典的图算法深入介绍这个框架的具体应用，在复杂度的分析中，PFS由两层循环构成，其中内层循环又含并列的两个循环，采用邻接表的方式，总体的复杂度为O（n^2)

3.4 最小支撑树

连通图G的某一无环连通子树T若覆盖G中所有的顶点，则称为G的一颗支撑树或生成树（spanning tree）

就保留原图中边的数目而言，支撑树是禁止环路前提下的极大子图，也是保持连通前提下的最小子图，其往往对应系统中最经济的连接方案

3.4.1 蛮力算法

3.4.2 prim算法（属于PFS的特例，时间复杂度为O（n^ 2）

3.5 最短路径树

可以看下面问题描述

Dijkstra算法（时间复杂度O(n^2)

0x04 交通运筹学中的图的应用

4.1 最短路径问题

在生产实践、运输管理和工程时间的很多活动中都需要面临寻找“图的最短路径”，这是网络规划中的一个基本问题

假设对于有向图D=（V，E），设图D的每条边(u,v)都和一个实数权重W（e）=W（u，v）对应，则称为赋权图。这里所说的权是与边有关的数量指标，可以根据问题的需要不同的含义，比如距离、时间和费用等

$W（P）=\Sigma W(e)$

常见的解决方法

4.1.1 Dijkstra算法(略)

4.1.2 Bellman-Ford算法（略

4.2 最长路径问题

4.3 第k短路径问题

在最短路径的基础上，考虑第k路径感兴趣

4.4 最小生成树

给定连通赋权无向图G=（V，E），若T为G的生成树，T中边e的权

$W(T)=\Sigma W(e)$

其中最小的称为最小生成树，一些常见的算法

4.4.1 Prim算法（略）

4.4.2 Kruskal 算法（略）

4.5 中国邮路问题

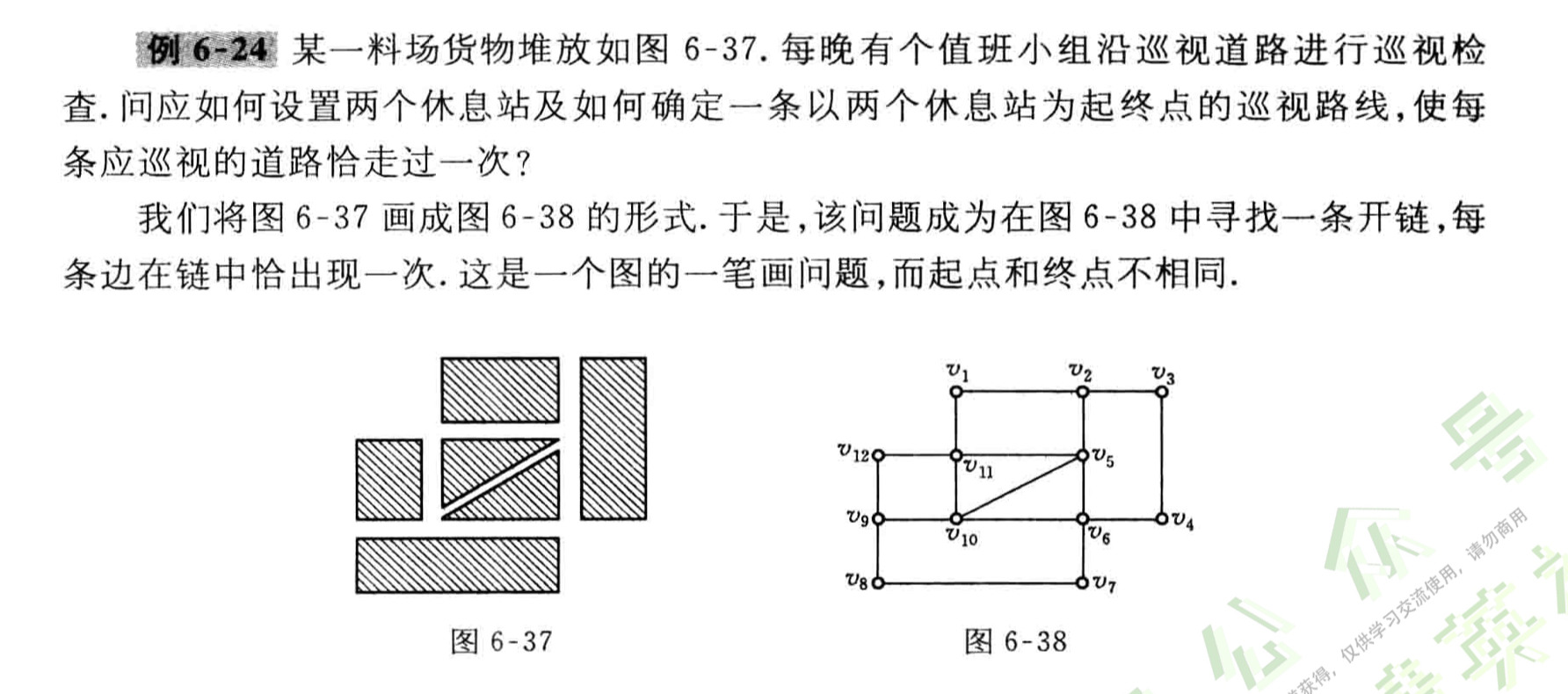
4.6 运输网络

许多系统中存在流的问题，运输系统有物资流、公交系统中有车辆流、供水系统中存在水流，因此可以用图来描述网络，因此给定一些数学定义

运输网络

网络流

添加图片注释，不超过 140 字（可选）

最小割

添加图片注释，不超过 140 字（可选）

最大流

添加图片注释，不超过 140 字（可选）

4.7 最大流（4.6）

4.8 最小代价流问题（4.6）

程序设计

#图 graph

数据结构和算法设计 Vol2

https://blog.tjdata.site/posts/a3119115.html

作者

chenlongxu

发布于

2024年4月29日

许可协议

Pyomo 简单示例学习上一篇

数据结构和算法设计 Vol1 下一篇

数据结构和算法设计 Vol2

0x01 数据结构中的 图 Graph

1.1 概述

1.2 抽象数据类型的实现

1.3 邻接矩阵 Adjacent matrix

1.3.1 时间性能

1.3.2 空间性能

1.4 邻接表（adjacent list）

1.4.1 时间复杂度分析

1.4.2 空间复杂度分析

1.5 图（Graph）遍历算法概述–BFS和DFS

1.5.1 广度优先搜索 breadth-first-search BFS 越早被访问到的顶点，其邻居被优先选用

0x02 交通运筹学中的图

2.1 交通中图的例子

2.2 基本概念–无向图G

2.3 基本概念–有向图D

2.4 基本概念–矩阵表示

2.5 树

0x03 数据结构中图的应用

3.1 拓扑排序（topological sorting）

3.2 双连通域分解

3.3 优先级搜索

3.4 最小支撑树

3.4.1 蛮力算法

3.4.2 prim算法（属于PFS的特例，时间复杂度为O（n^ 2）

3.5 最短路径树

0x04 交通运筹学中的图的应用

4.1 最短路径问题

4.1.1 Dijkstra算法(略)

4.1.2 Bellman-Ford算法（略

4.2 最长路径问题

4.3 第k短路径问题

4.4 最小生成树

4.4.1 Prim算法（略）

4.4.2 Kruskal 算法（略）

4.5 中国邮路问题

4.6 运输网络

4.7 最大流（4.6）

4.8 最小代价流问题（4.6）

0x01 数据结构中的图 Graph