数据结构和算法设计 Vol1

这里主要借鉴Tsinghua的2020fall<数据结构与算法>这本书，包含对于一些基本数据结构的探索，先从定义梳理，在整理题目，之后是实际训练。结合之前在程序设计或嵌入式中对于数据在实际存储的例子来学习可能会更好。从中也能体悟到算法一些含义

本次主要对绪论、线性结构的数组（Array）为基础的向量（Vector）、以链表（Link）为基础的列表（List）、栈（Stack）与队列（Queue）；半线性结构的数（Tree）、非线形结构的图（Graph）做定义的记录和梳理。

Chapter01 绪论

1.1 瞎说

计算机是人类从事计算的工具，也是抽象计算模型的具体物化，基于图灵模型的现代计算机，即是人类现代文明的标志与基础，更是人脑思维的拓展与延伸。尽管计算机的性能日益提高，但是这种能力在解决实际应用问题能够真正得到发挥，决定性的因素在于人类如何深入思考与分析获得对问题本质的透彻理解，

• 需要按照长期积淀的框架和模式来设计出合乎问题内在规律的算法，
• 选用、改进或者定制足以支撑算法高效实现的数据结构，
• 并在真实的应用环境中充分测试、调试和改进

那么什么是算法？

• 埃及人的绳索是算法
• 尺规作图是算法
• 冒泡排序bubble sort也是算法

宏观的定义是基于特定的计算模型，在解决某一信息处理问题而设计的一个指令序列，本书所说的算法还需要具有以下的特点

• 有input和output
• 可操作、确定性与可行性
• 有穷性和正确性，finiteness and correctness
• 退化与鲁棒性，degeneracy and robustness
• 重用性，reuse

如何评价一个算法呢？

• 可计算性computability
• 难解性 intractability，本书将更多的关注于非“不可解和难解”的一般性问题，并讨论如何效率的解决这一层面的计算问题，因此需要确定一种尺度，从时间和空间方面度量算法的计算成本，并由此对不同算法进行比较和评判，当然最重要的是在研究和归纳算法设计月实现过程中的一般性规律与技巧，以编写出效率更高、能够处理更大规模数据的程序，这是本书的基本主题也是贯穿主题的脉络
• 计算效率
• 数据结构

1.2 复杂度complexity度量

时间复杂度（Time complexity），运行时间是由多种综合因素作用而决定的，因为对于同种算法，对于不同的输入所需的运行时间并不相同，比如对于排序问题，输入序列的规模其中各元素的元素以及次序均不确定，这些因素都将影响到排序算法最终的运行时间，因此为来运行时间建立一种可行、可信的评估标准，需要考虑其中的关键因素 因此可以将这个问题转化成为：随着输入模式的扩大，算法的执行时间将如何增长？执行时间的这一变化趋势可表示为输入模式的一个函数，可以讲起称为时间复杂度time complexity，对于特定算法处理规模为n的问题所需要的时间可以作T(n) 渐进复杂度（asymptotic analysis），一些算法适用于小规模输入，一些算法适用于大规模输入，在评价算法运行效率时，我们往往可以忽略其处理小规模问题的差异，转而关注在处理更大规模问题时的表现，在其中我们可以尝试用一些方法，1. 大O记号 2 大Omega记号 3 大Theta记号

1. 渐进上界 ，也就是最差情况big-O notation，对于规模为n的任意输入，算法的运行时间都不高于O（f（n））
2. 渐进下界，也就是最好情况big-Omega-Notation，对于规模为n的任意输入，算法的运行时间都不低于Omega（g（n））
3. 如果恰好渐进上界和渐进下界之间先等，O=Omega，因此可以使用big-theta-notation做记号

添加图片注释，不超过 140 字（可选）

空间复杂度（space complexity），为了更加客观地评价算法性能的优劣，除非特别申明，空间复杂度通常并不原始输入本身所占用的空间，对于同一问题，这一指标对任何算法都是相同的，反之其他的各种方面所小孩的空间都应该计算

另外在很多时候我们都是更好甚至仅仅关注于算法的时间复杂度，而不必对空间复杂度多专门的考察，这种简单评测方式的一句都来自于一下事实：就渐进复杂度的意义而言，在任一算法的任何一次运行过程中所消耗的存储空间都不会多余期间所执行基本操作的累计次数；但是空间复杂度的分析的意义在于对空间效率非常在乎的应用场合中，当问题的输入规模极为庞大时，由时间复杂度所确立的平凡上界已经难以令人满意

1.3 复杂度分析

在1.2 中确定算法复杂度的度量标准，分析算法的复杂度，可一般使用大O算法，来将各种算法的复杂度从低到高划分为不同的级别

• 常数O（1）
• 对数O(log N)
• 线性 O（n）
• 多项式 O（polynomial（n））
• 指数O（2^n）

1.4 递归recursive

递归的价值在于，许多应用问题都可以简介而准确地描述为递归形式，同时也是一种基本而典型的算法设计模型，这模式可以对实际问题中反复出现的结构和形式loop variant进行高度概括，并从本质层面加以描述与刻画，进而导出高效的算法

本篇文章从递归的基本模式入手，循序渐进介绍如何选择和应用（线性递归、二分递归和多分支递归等）不同的递归形式，来实现（遍历、分治等）算法策略，以及如何利用递归跟踪和递推方程等方法分析递归算法的复杂度

• 线性递归，base case of recursion，避免因无限递归导致系统溢出，往往对应减而治之decrease and conquer的算法策略，递归每深入一层，待求解问题的规模都缩减一个常熟，直至最终蜕化为平凡的简单问题
• 递归分析，可以使用递归跟踪与递归方程两种主要的方法
• 算法的每一个递归实例都表示为一个方框，其中著名该实例调用的参数
• 若实例M调用实例N，则在M与N对应的方框之间添加一条有向联线
• 递归模式
• 递归消除
• 二分递归 divide-and-conquer

Chapter02 （Static）向量vector

数据结构是数据项的结构化集合，其结构表现为数据项之间的相互系列与作用，也可以理解为定义与数据项之间的某种逻辑次序，根据这种逻辑次序的复杂程度，可以将数据结构划分为线性结构、半线性结构和非线性结构三个部分

在线性结构中，数据项按照一个线性次数构成一个整体，其中最基本的线性结构为sequence，根据数据项的逻辑次序和物理存储地址的不同可以区分为向量vector和列表list

本章的讲解将围绕向量结构的高效实现而逐步展开，包括作为抽象数据类型的接口规范以及对应的额算法，尤其是高效维护动态向量的技巧

2.1 从数组和向量

数组 Array

若集合S由n个元素组成，且各元素之间具有一个线性次序，则可以将他们存在在开始地址A、物理位置连续的一段存储空间，

$A=[a_0,a_1,…,a_{n-1}]$

q其中i小于j，A[i]都是A[j]的predecessor，后者是successor，相邻的成为immediate predecessor；immediate successor，元素的所有前去构成前缀prefix，所有的后继构成suffix

采用这样的元素规范，不仅使得每个元素都通过下标唯一指代，而且可以让我们直接访问任何元素，这里所说的访问包括 读取和修改等基本操作，“直接”的意思是这些操作可以在常数时间内完成

在其中元素的物理地址与其下标之间满足这种线性关系，因此被称作Linear Array

向量Vector

对数组array基础上做一般性的推广。也是具有线性次序的一组元素构成的集合

$V=[v_0,v_1,…,v_{n-1}]$其中的元素分别由Rank秩相互区分

在这样抽象之后，我们不在限定同一个向量中的元素都属于同一基本类型，本身可以是来自于更具一般性的某一类的对象，另外各元素也不见得同时具有某一数值属性，故并不保证之间可以相互比较大小

2.2 Interface接口

操作接口

具有一些基本操作，

添加图片注释，不超过 140 字（可选）

介绍其中某些操作，比如size（）、get（）等静态操作可以在常数时间内完成

insert（）、remove（）等动态操作可能需要线性时间

Chapter03 （Dynamic）列表List

上一个章节中的元素访问为call-by-rank访问

另外一种形象的元素访问时间可以是call-by-link

不同数据结构内部的存储与组织方式差异，其操作接口的作用方式和时空性能也不相同，在设计和选用数据结构时，应该从实际应用的需求出发，先确定功能规范及性能指标，比如引入LIst的目的就是为了弥补Vector在解决某些应用问题的功能和性能方面的不足，两者之间的差异体现在对外的操作不同，根源在于内部存储方式的不同

3.1 从Vector到List

这也代表这从Static到Dynamic之间的转变

Static Storage Policy 静态存储策略

之前的Vector采用的就是静态存储的策略，“各元素物理地址连续”，由此导致的size（）get（）静态操作均可以在常数时间完成，而insert（）、remove（）等动态操作却都可能需要线性时间；得益于这种策略，我们可以O（1）时间内由Rank确定向量元素的物理地址，但是反过来在insert和remove的 过程中又不得不移动 O（n）元素，可以看出静态存储策略的静态操作的效率达到了极致，但是动态操作，局部的修改会引起整个范围甚至整个数据结构的调整

Dynamic Storage Policy 动态存储策略

List作为代表，尽管要求元素在逻辑上具有线性次序，但对物理地址并未做出任何限制，具体的是在生命周期内，此类数据结构将随着内部数据的需要，相应分配或回收局部的数据空间，如此元素之间的逻辑关系得以延续，却不必与物理次序相关，作为补偿，这类结构将通过指针或引用等机制来确定各元素的实际物理地址

比如链表（Linked list）就是一种典型的动态存储结构，其中的数据分散为一系列称为节点（Node）的单位，节点之间通过指针相互索引和访问，引入新的节点就可以删除原有的节点，在局部调整少量相关节点之间的指针

但是这样并不是没有问题

在提高动态动态操作效率的同时，却不不得不舍弃原静态存储策略中使用Rank访问的方式，从而造成来静态操作性能的下降，虽然Link list的访问可以通过Rank来查询，但是其本质上是通过多次的指针递归得到的，因此平均访问时间为O（n）

Chapter04 （更基本）栈Stack 与队列Queue

本章的目标是实现更加基本，也更加常用的两类数据结构—栈和队列，属于线性序列结构，古其中存放的数据对象之间也具有线性次序，相对于一般的序列结构，栈与队列的数据操作范围仅限于逻辑上的特定某段，得益于其简洁行于规范性，他们可以构建更复杂、更高级数据结构的基础，也是算法设计的基本方法

相对于向量和列表，栈于队列的外部接口更为简化和紧凑，得益于此，本章的重点将不在拘泥对数据结构内部实现机制的展现，并转而更多从外部特性出发，结合若干典型的实际问题介绍栈和队列的具体应用

在队列的应用方面，贲张将介绍如何实现基于轮值策略的通用循环分配器，并以银行窗口服务为例实现基本的调度算法

4.1 栈（Stack）

栈是存放数据对象的一种特殊容器，其中数据元素按照线性逻辑次序排列，因此可以定义首、末元素，不过尽管栈结构也支持对象的插入和删除操作，其操作的范围仅限于栈的某一特定端，也就是说，若约定的元素只能从某一端插入其中，则反过来也只能从这一端删除已有的元素

类似于这种操作，栈中可以操作的一段成为栈顶Stack Top，另一段无法直接操作的盲端称为Stack Bottom，最常用的插入和删除操作分别称为入栈Push和出栈Pop

4.2 栈与递归

递归算法所需的空间量主要决定于最大递归深度，在达到这个深度的时刻，同时活跃的递归实例达到最多，

关于操作系统是如何实现函数递归调用的？如何记录调用与被调用函数（递归）之间的关系？如何实现函数（递归）调用的返回？又是如何维护同时活跃的所有函数（递归）实例的实现的？

这些所有问题的答案，都可以归结于栈Stack

在windows操作系统中，每个运行中的binary executable的二进制程序都配有一个调用栈（call stack）或执行栈execution stack，借助调用栈可以跟踪属于同一程序的所有函数，记录它们之间的相互调用关系，并保证在每一调用实例执行完毕之后，可以准确返回

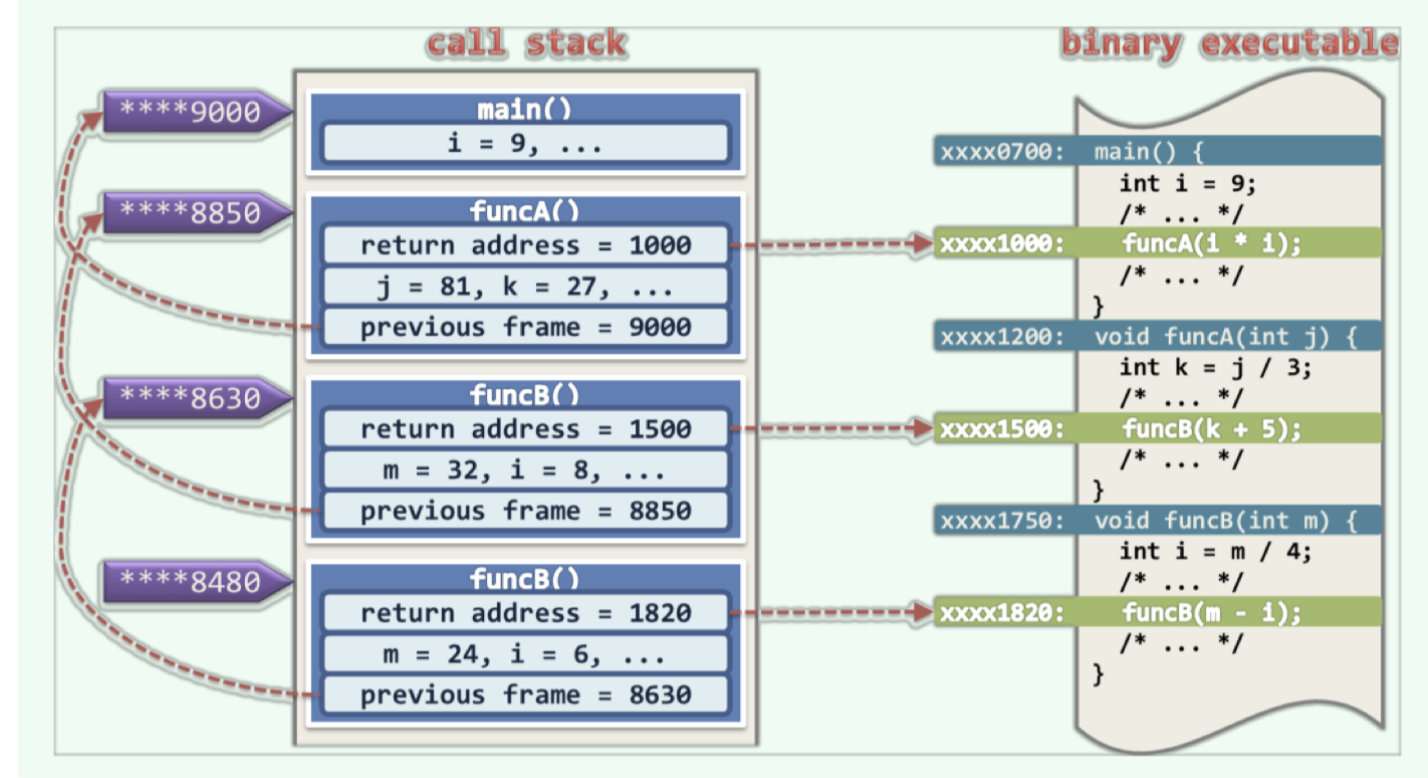
添加图片注释，不超过 140 字（可选）

• 函数调用

Call Stack的基本单位是帧（Frame）、以及局部变量、输入参数，并将该栈Push调用栈，并在该函数返回之前发生新的调用，同样将与新函数对应的一帧Push栈顶，函数一旦运行完毕，对应的帧随即弹出，运行控制权将被交还给该函数的上层调用，并按照Frame记录的返回地址确定二进制程序中继续执行的位置，当位于栈底的main（）被弹出意味着整个程序的运行结束，此后控制权将交还给OS

CPU眼里的：{函数} | 栈帧 | 堆栈 | 栈变量 | 调用栈_哔哩哔哩_bilibili

• 递归

作为函数调用的特殊形式，递归也可以借助上述调用栈得以实现，可以看出同一函数可能同时拥有多个实例，并在调用栈中各自占有一栈，这些栈的结构完全相同

一些没有用的建议

4.3 栈的典型应用

4.3.1 逆序输出

逆序输出中的共同特征：首先，虽有明确的算法，但解答却以线性序列的形式给出，其次无论是递归还是迭代实现，该序列都是按照逆序计算输出的，最后输入和输出规模不确定，事先难以确定盛放输出数据的容器大小，因此具有特有的“后进先出”的特点，以及在容量方面的自适应性，因此可以使用Stack来解决这类问题

进制转换问题，可以将十进制整数n转换为lambda进制的表现形式

比较简单的除呗

void convert(S,int：n,base){
    static char digit[]={'0','1',...,'E','F'};
    if (n>0){
    S.push(digit[n%base]}
    convert(S,n/base,base)//在C中这里的n/base会自动输出为整数
}
}
//新的base进制下由高到低的各数位，自顶而下保存与栈S中

4.3.2 递归嵌套

具有自相似性的问题可以用多嵌套递归描述，但因为分支位置和嵌套深度并不固定，其递归算法的复杂度不易控制，栈结构及其操作天然具有递归嵌套性，因此可用于高效解决这类问题

栈混洗（Stack Permutation）

假设三个栈A、B、S，其中BS开始为空，A中包含n元素，S作为中间转移栈，将A中元素转移到B中，其中仅允许

S.Push(A.Pop())

B.Push(S.Pop())

括号匹配问题，对源程序的检查是代码compile中重要而基本的一个步骤，而对表达式括号匹配的检查又是语法检查中必需的一个环节 其任务是，对任何一个程序块，需要判断其中的括号是否在嵌套的意义下完全匹配，

4.4 试探回溯法（Probing and BackTracking）

古希腊神话中半人半牛的怪物弥诺陶洛斯（Minotaur），藏身于一个精心设计、结构极其 复杂的迷宫之中。因此，找到并消灭它绝非易事，而此后如何顺利返回而不致困死更是一个难题。 不过，在公主阿里阿德涅（Ariadne）的帮助下，英雄忒修斯（Theseus）还是想出了个好办法， 他最终消灭了怪物，并带着公主轻松地走出迷宫。

实际上，忒修斯所使用的法宝，只不过是一团普通的线绳。他将线绳的一端系在迷宫的入口 处，而在此后不断检查各个角落的过程中，线团始终握在他的手中。线团或收或放，跟随着忒修 斯穿梭于蜿蜒曲折的迷宫之中，确保他不致迷路。

忒修斯的高招，与现代计算机中求解很多问题的算法异曲同工。事实上，很多应用问题的解， 在形式上都可看作若干元素按特定次序构成的一个序列。 以 经典 的旅行商问题（ traveling salesman problem, TSP）为例，其目标是计算出由给定的n个城市构成的一个序列，使得按此 序列对这些城市的环游成本（比如机票价格）最低。尽管此类问题本身的描述并不复杂，但遗憾 的是，由于所涉及元素（比如城市）的每一排列都是一个候选解，它们往往构成一个极大的搜索 空间。通常，其搜索空间的规模与全排列总数大体相当，为n! = O(nn )。因此若采用蛮力策略， 逐一生成可能的候选解并检查其是否合理，则必然无法将运行时间控制在多项式的范围以内。

这样的算法对应这样的模式：

从零开始，尝试逐步增加候选解的长度，更准确地是在这个过程中成批的考察具有特定前缀的所有候选解，这种从长度上逐步向目标解靠近的尝试，成为试探 Probing

作为解得到局部特征，特征前缀在试探的过程中一旦被发现与目标解不适合，则收缩到此前一步的长度，然后试探下一可能的组合，特征前缀长度缩减的这类操作成为，回溯BackTracking，其效果等同于剪枝Pruning

在上述的故事中，这种方法依赖于有型的物质基础，也就是需要保证搜索过的过程不被重复搜索，办法就是在剪枝的位置留下某种标记

八皇后，国际象棋中皇后的势力范围覆盖所在的水平线、垂直线和两条对角线，现在考察如下的问题 在n*n的棋盘中，如何使得她们之间彼此互不攻击， 此时称她们构成一个可行的棋局，对于任何整数n大于等于4

首先分析问题可以看出，n皇后可以在n*n的棋盘上可行，首先需要设计Queen这个类，也就是坐标，通过重载判断等操作符来实现对皇后位置是否相互冲突的便捷判断

若每行能且只能放置一个皇后，不妨首先将每个皇后分配给每一行，然后从空棋盘开始逐个尝试将她们放置到无冲突的某列，没放置好一个皇后才继续试探下一个，若当前皇后在任何列都会造成冲突，则后续皇后的试探都是徒劳的，因此应该回溯到上一皇后

可以借助栈solu来动态记录各皇后的列号，当该栈的规模增至N得到全局解

添加图片注释，不超过 140 字（可选）

迷宫寻路，要求依照预定的行进规则，在具有特定集合结构的空间区域内，找到从起点到终点的一条通路，这样的简化版本 在空间区域限定为由n*n的方格组成的迷宫，除来四周的围墙，还有分布其间的若干障碍物，只能水平或垂直移动 我们的任务是在任意制定的Origin和Des中找到一条通路

4.5 队列Queue

与栈Stack一样，队列Queue也是存放数据对象的一种容器，其中的数据对象也按照线性的逻辑次序排列，队列结构同样支持对象Insert和delete，但是两种操作的范围分别被限制于队列的两端（若约定新对象只能从某一端插入其中，则只能从另一端删除已有的元素，允许取出元素的一端成为队头Front，而允许插入元素的另一端成为队尾Rear

对于的插入和删除操作，从队的角度可以称为enqueue和dequeue的操作

对应的一些基本操作

循环分配器，为在客户client群体共享某一资源，比如共享CPU，一套公平且高效的分配规则必不可少，而队列结构则非常适于定义和实现这样的一套分配规则

可以使用所谓的轮值round robin算法中，首先令所有参与资源分配的客户组成一个队列Q，接下来是一个反复轮回式的调度过程

这里，每位用户持续占用资源的时间对算法的成败至关重要，一方面，未来保证响应速度，这个时间值通常不能过大；另一方面，因占有权限的切换也需要消耗一定时间，因此这个时间取的过小，切换过于频繁也会造成整体效率的下降

银行服务模拟，介绍如何使用Queue结构实现顾客服务的调度于优化，

Chapter05 二叉树 Tree

如果以平衡二叉搜索数为例子，若其中包含n个元素，则每次查找、更新、插入和删除操作等都可以在O(log N)的时间内完成

数结构有不计其数的变种，在算法理论以及实际应用中扮演着最为关键的角色，得益于独特而又普适的逻辑结构。树作为一种分层结构，而层次化这个特征几乎蕴含在所有食物及其联系之中

作为树的特例，二叉树实际上并不失其一般性，就本章而言，无论是逻辑结构还是算法功能来说，任何有跟有序的多叉树都可以等价转化并实现为二叉树，本章的终点在二叉树中，我们将用通讯编码算法的实现这个应用实例作为线索贯穿全章

5.1 二叉树及其表示

5.1.1 树（Tree）

从图论的角度来看，树等价于连通无环图，因此与一般的图相同，树可以用

• 一组定点Vertex，及其连接与其间的若干条边edge组成
• 在计算机科学，在这个基础上在制定某一特定定点成为根root，实现rooted tree
• 在程序实现的角度上，更多将定点vertex称做节点node

由于树的连通性，每个节点与根之间都有一条路相连，而根据树的无环性，由根通往每个节点的路径必然唯一，因此在每个节点vertex到根root的唯一通路所经过边的数目，称作的深度depth，依据深度排序可以对所有节点做分层归类

• depth；沿每个节点vertex到根root的唯一通路所经过边的数目成为该节点的深度
• 祖先ancestor/后代descendant；这个是包含vertex节点本身
• 真祖先proper ancestor/真后代proper descendant；不包含vertex节点本身
• parent/child；相邻的成为父母节点，和孩子节点
• degree，vertex的孩子总数称为度树或者度，记做deg（v）
• leaf，无孩子的节点被成为叶节点，包括根在内的其余节点都被称内部节点internal node
• subtree；vertex的所有后代及其之间的联边称作子树，subtree（v）

5.1.2 二叉树 （Binary Tree）

二叉树中的每个节点的degree均不超过2，因此在Binary Tree中同一父节点中的汉子都可以使用左、右相互区分，因此可以被称为有序二叉（Ordered Binary Tree）；特别的，不包含一度节点的二叉树称为真二叉树（Proper Binary Tree）

5.1.3 多叉树（K-ary Tree）

一般来说，树中各节点的degree的数目并不确定，每个节点的degree均不超过k个的有根树，称为K叉树

在这个过程过，多叉树的表现方式有多种

1. 父节点表示方法
2. 孩子节点表示方法
3. 父节点和孩子节点表示方法
4. 有序多叉树=二叉树
5. 长子和兄弟
6. 父节点表示方法

可以将各节点组织为向量Vector或列表List，其中每个元素除保存节点本身的信息Data之外，还需要保存父节点Parent的Rank或Position

特别的，可以为Root指定一个虚构的父节点-1或Null，便于统一判断

如此，所有向量或列表所占的空间总量为O（N），线性正比于节点总数N，时间方面，仅需常数时间就可以确定任一节点的父节点Parent；但是反过来，孩子节点的查找却不得不花费O（n）时间访遍所有节点

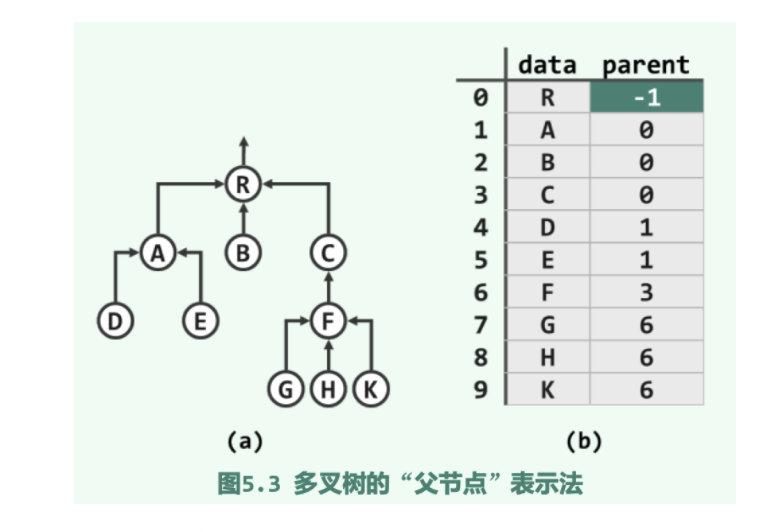
添加图片注释，不超过 140 字（可选）

• 孩子节点表示方法

可以让每个节点将其所有的孩子组织为一个向量或列表，由此对于拥有r个孩子的节点，可以在O（r+1）的时间内列举出其所有的孩子

• 父节点和孩子节点

上面两种方式各有所长，也各有所短，为了综合两者之间的优势，消除缺点，可以使用各节点记录父节点，也记录序列保存所有孩子

但是这种方法并不是没有缺点；尽管如此可以高效兼顾对父节点和孩子定位，但在节点插入与删除操作频繁的场合，为了动态维护和更新树的拓扑结构，不得不反复遍历和调整一些节点所对应的孩子序列，然而Vector和List等线性结构的此类操作都需要耗费大量时间，势必影响到整体的效率

• 有序多叉树和二叉树

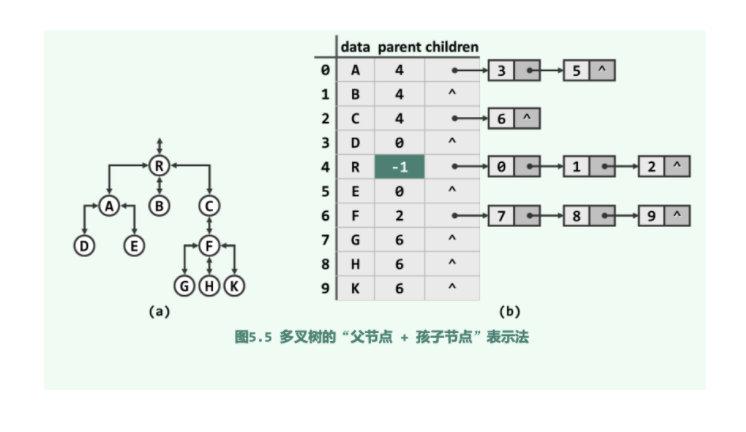
添加图片注释，不超过 140 字（可选）

采用从支持高效动态调整的二叉树结构，为此必须首先建立从多叉树到二叉树之间的某种转换关系，在这种转换的意义下，任何多叉树都等价与某颗二叉树

• 长子和兄弟

多序多叉树中任一非叶节点都有唯一的长子，而且可以该长子出发，按照约定或指定的次序遍历所有的孩子节点

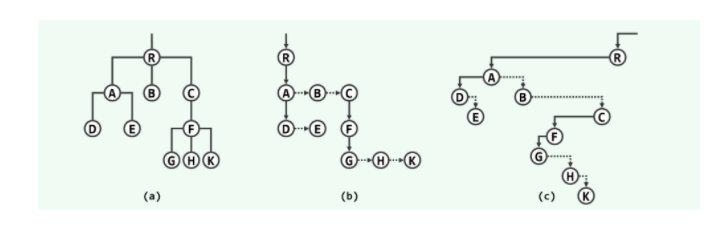
添加图片注释，不超过 140 字（可选）

一个非常有趣的现象出现：尽管二叉树只是多叉树的一个子集，但是对应用问题的描述和刻画能力并不低于后者，实际上以下我们还能进一步发现，即便就计算效率而言，二叉树也并不逊色一般意义上的树，反过来，得益与定义的简洁性以及结构的规范性，二叉树所所支撑的算法往往可以更好地得到描述，更加便捷实现

5.2 编码树

通过将通讯编码算法的实现作为二叉树的应用实例，通讯理论的基本问题是在尽可能低的成本下，用最高的速度来真实的实现信息在空间和时间上的复制和转移；在信道转移的信息大多按照二进制比特形式表示和存在，而每一个具体的编码方案都对应一颗二叉编码树

讲解的不深，不值得看，可以去看《信息传输远离》

5.3 二叉树的实现

作为图（Graph）的特殊形式，二叉树的基本组成单元是节点与边，作为数据结构，其基本的组成实体是二叉树节点（Binary Tree Node），边作用与节点之间的相互作用

Chapter06 图 Graph

例如之前例子中的迷宫，借助绳索掌握迷宫内各通道之间的相互关系，在很多应用中我们需要准确有效描述和利用这类信息，这类信息往往可以表述为定义与一组对象之间的二元关系，比如城市交通图、比如互联网中的IP地址，尽管上一章的树 Tree结构也可以用来表示这种二元关系，但是仅限与Parent Node 和Child Node之间，这种一般性的二元关系属于图论 Graph Theory的范畴

本章的主要目的

1. 简要介绍Graph的基本概念和术语
2. 如何实现作为抽象数据类型的图结构，主要讨论邻接矩阵，和邻接表两种实现方式
3. 从遍历的调度介绍将图转换为树的典型方法，包括广度优先搜索和深度优先搜索
4. 分别以拓扑排序和双连通域分解为例子，介绍利用基本数据结构并基于遍历模式，设计图算法的主要方法
5. （数据结构决定遍历次序）的观点出发，将遍历算法概括并统一为最佳优先遍历这一模式，如此来更加准确和深刻理解不同图算法之间的共性与联系，更可以学会通过选择和改进数据结构，高效设计并实现各种图算法

6.1 概述

6.1.1 图

图（Graph）定义为G=（V，E）。集合V中的元素为顶点Vertex，集合E中的元素分别对应于V总的某一对顶点（u,v），表示它们之间存在的某种关系，因此可以称为边（Edge），从计算需求的角度约定都是有限集，规模分别记为n和e

• 无向图undirected graph，若边(u,v)所对应顶点的u和v的次序无所谓，称作无向边direct edge；
• 有向图directed graph。如果不对等，称为directed edge，如果从u指向v，则其中u是该边的origin或者尾顶点tail，v是该边的终点destination或头顶点head
• 如果包含有向边和无向边，可以称为混合图mixed graph

度（Degree），对于任何一边e=，可以称顶点u和v彼此邻接（adjacent），同时与边e彼此关联（incident）。在无向图中，与顶点v关联的边数称为v的度数（degree），记deg（v）；在有向图中，出边总数称为出度（out-degree）、入边总数称为（in-degree）

简单图，是联接与同一顶点之间的边，称为自环self-loop，在某些特定的应用，这类边的确具有意义，但是不含任何自环的图称为简单图 simple graph

（之后巴拉巴拉一大堆。。。掠过）

带权网络（weighted network，G（V，E，wt（）））需要通过一个权值函数，为每一边e指定一个权重weight，wt（e）指定边e的权重

复杂度（complexity），在这个过程中n各顶点，最多有e=O（n^2)来进行描述