Combining_Reinforcement_Learning_and Constraint_Programming_for_Combinatorial Optimization
将RL嵌入到现有的框架当中来保证效率和完全性,非常Fancy!
https://arxiv.org/abs/2006.01610
Abstract
Combinatorial Optimization 应用广泛:从航空领域、交通规划甚至到经济学中,它的目标是在有限的解空间中找到最优解(find an optimal solution among a finite set of possibilities),其面临的最严重的挑战为Q-state-action方法 中提到的 状态空间爆炸(State- space explosion problem):问题的解空间岁问题规模增大成指数型的增大,导致对于一些大型的问题难以求解;另一方面DRL(deep reinforcement learning)在求解NP-hard 组合优化问题过程对设计好的启发式求解算法具有比较好的贡献,但是现有的方法具有两个缺点
- 他们仅仅专注于标准的TSP问题,不容易拓展到其他问题
- 通常只给出一种近似解(approximate solution),而没有给出一种系统的方法来提高或者证明它的最优性(Optimality)
在另外一种情况下,Constraint programming 是解决组合优化问题的通用工具,基于一个完整的搜索过程,通常可以在比较大的运行时间中找到最优解。其中决定性的确定搜索的方向,或者说分枝策略,或者说是探索策略。
在本文中我们提出一种通用和混合的方法(l)的方法,结合CP和DRL来求解COP,主要是基于运筹学Part01–dynamic programming 作为两者之间的桥梁,并通过实验来证明求解器在两个有挑战性的问题上进行求解:TSPTW the traveling salesman problem with time windows 和 4POP 4-moments portfolio optimization problem,实时证明比一些单独的RL或者利用通用求解器效果更好
Brief Conclusion P:具有多项式时间算法,算得很快的问题 NP:不确定需要多长时间,但是我们验证它只需要多项式时间 NP- complete:属于NP问题,同时也属于NP-hard问题 NP-hard:比NP问题都要难的问题
NP问题 指的是非确定性多项式问题(non- deterministic polynomial NP),非确定性指的是可用一定数量的运算去解决多项式时间内可解决的问题,通常解决问题包括:TSP、Hamilton回路问题、最大团问题;但是其可以在多项式时间内可以被验证其正确定的问题
NP-hard问题 指的是non- deterministic polynomial time hardness,如果所有的NP问题都可以在多项式时间规约到某个问题,则称这个问题为NP困难
Introduction
在组合优化中大多数问题为NP-hard问题,对其高效的优化算法的探索由来已久。广泛的可以将其分为两种方法
精确算法 exact algorithm 是基于对求解空间的完整并且巧妙的枚举,它的优点是可以选招到最优解,但是在对于一些大型的案例中往往会出现求解时间扩大。但也有另外的说法可以让精确算法在找到最优解之前就终止的方式来探索得到次优解。这种灵活性让精确求解算法更加appealing并且practical,也正是如此构成了现代求解器的核心 CPLEX、Gurobi、Gecode等等。这是一个CP的介绍,通过additional asset 用来求解非常大的复杂性的COP问题,通常混合整数规划mixed integer programming MIP 求解器往往只能求解线性问题或者有限的非线形问题。
Handbook of Constraint Programming
而在利用CP进行求解的过程中重要的是branching strategy,非常自然的,好的设计的启发式的探索方法可以很好的发现求解,但是差的启发式分枝策略往往会导致进入没有解的子空间。所以在CP求解问题中br分枝策略的研究是非常热门的话题
启发式算法 heuristic algorithm 是一种非完全的手段来求解得到最终解,但是不能证明解的最优性。他们通常需要特定子问题的知识才能构建他们。在近几年,Lecture01 Deep Reinforcement Learning, Decision Making,and Control 在对一些NP-hard的COP问题的近似求解中取得了非常好的成果。只要一个模型训练好,在实践中的运行时间是可以忽略不计的,利用DRL求解问题的前提是
- 我们知道实际问题的例子分布
- 我们有足够多的样本,并可以从中采样来训练模型
但是现有的DRL在COP应用中存在的一些问题表阔
- 仅限于求解特定的问题,比如TSP
- 其次,它们仅旨在充当建设性的启发式方法,并且与完整的方法(例如CP)不同,没有系统的方法来改进所获得的解决方案。
上述的精确算法 exact algorithm 和基于学习的启发式算法 heuristic algorithm 都具有好处和坏处,很自然的就有一个问题
我们是否可以将他们的优点联合起来来求解COP
在本文中我们成果将RL与CP利用运筹学Part01–dynamic programming 结合起来,动态规划在很多场合中都具有很成果的作用,是一种非常关键的建模COP问题的方法,简单来说DP问题将一个问题分解成为子问题并通过递归公式(recursive formulation,比如常见的bellman equation结合起来),其中DP面临的苦难常常是 维度灾难问题:生成的子问题的数量呈指数级增长,以至于将它们全部存储在内存中变得不可行。
据我们所知是第一次在CP求解器中内置可学习的启发式探索,详细的贡献如下:
- 对于COP问题新的DP编码方式来利用RL求解和CP模型
- 利用两种常见的RL模型,DQL、PPO,训练数据集是从问题中随机抽样得到的
- 与现有的CP求解过程中分枝策结合,形成三种 brand and bound \ iterative limited discrpancy search and restart based search三种
- 给出有意义的结果
- 代码开源,为了简化后续研究的进程
通常如果没有内在的假设,比如线形和凸性,DP不能简单的编码然后利用标准的MIP方法求解,这也是驱动我们思考尝试使用CP进行编码的原因之一
下一章给出混合整数求解器求解的过程
对两个案例进行实验分析
最后给出总结
2 数据表征
这一部分总结我们提出的完整的框架,一个概括性的框架图在图一中展示,分为三个部分:
- 学习部分,利用随机生成的例子通过unifying representation作为RL的环境进行训练,最终训练的智能体是对求解过程中search的启发式分枝策略进行基于价值的选择(或者说是强化学习的探索)
- 求解部分,利用CP对模型进行求解,同时对求解的案例进行评估
- 联合表示阶段,讲输入的COP问题,结合Dominance pruning rules剪枝策略得到动态规划模型的建模,这样可以作为学习阶段的环境,也可以作为求解节点的输入模型
绿色表示我们的原创共享,蓝色表示已经有的框架
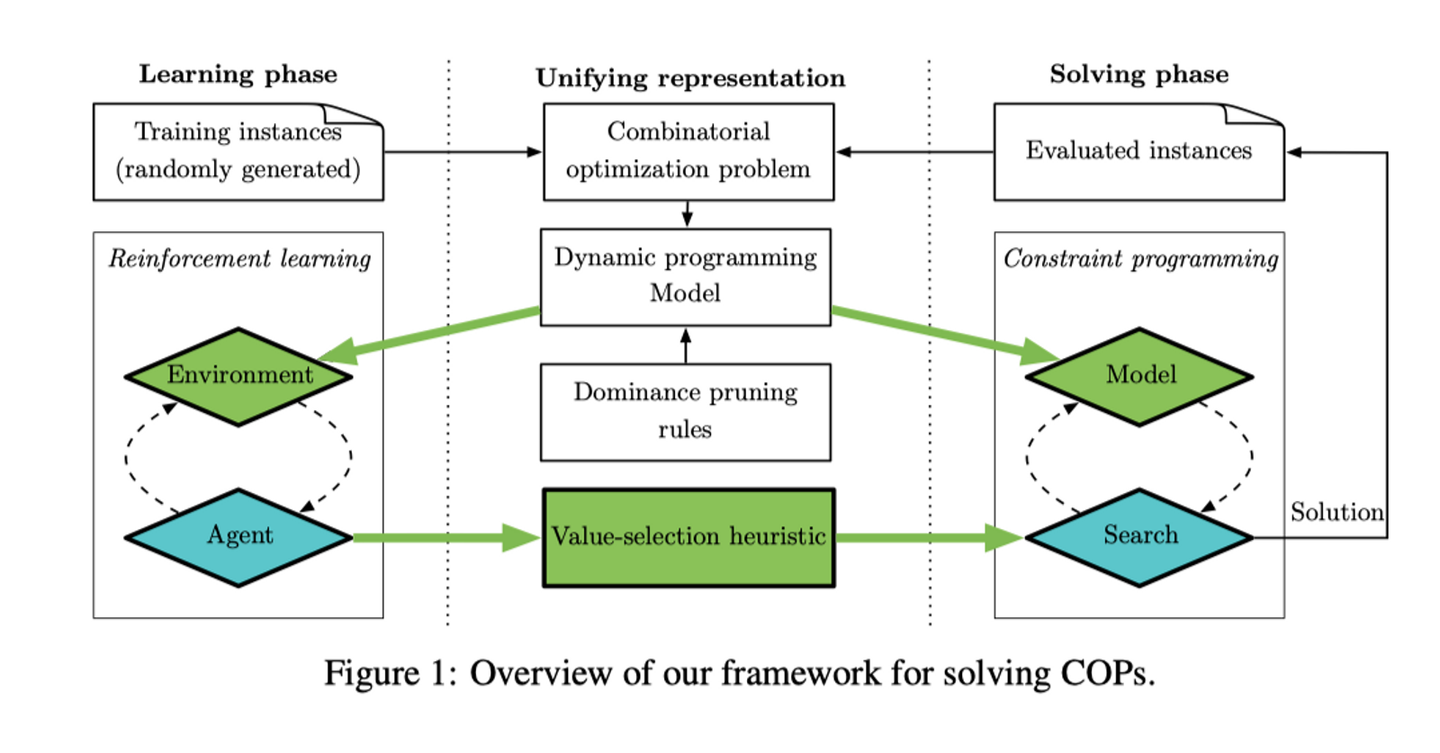
image-20221218154958762
2.1 动态规划模型
动态规划模型是一种将数学建模与计算机编程联系起来求解复杂优化问题的手段,简单来说是将一个大的问题转换成很多小的子问题然后将他们利用recursive formulation的方式联系起来最终求解,其中包括的一些关键的影响因素
| Q | COP问题 |
|---|---|
| controls | C |
| domain | D |
| transition | T |
| states | S |
| stage | |
| reward | R |
| validity conditions | V |
| dominance rules | P |
其中validity conditions 和dominance rules之间的区别在于两者之间的区别在于,有效性条件是强制性的,以确保DP模型的正确性(V (s, x) = 0 ⇔ T(s, x) = ⊥),而优势规则仅用于效率目的(P(s, x) = 0 ⇒ T(s, x) = ⊥),其中⇔、⇒和⊥表示等价性、含义、 和不可行的状态,分别。其中DP建模可以包括 S,X,T,R,V,P;根据贝尔曼方程我们可以一直计算到开头的状态的价值。
但是DP收到curse of dimensionality的影响,在解决大的状态或者动作空间下需要的内存很多,一种方法是对其进行剪枝处理,其中需要评估
此问题的部分解决方案是修剪主导操作 (P(s, x) = 0)。如果一个动作根据递归公式是有效的,那么它就是主导的,但(1)要么严格地比另一个动作差,要么(2)它不能导致可行的解决方案。在实践中,修剪这些主导操作会对搜索空间的大小产生巨大影响,但是在实践过程中找到这样的求解方案并不是容易的
而且就算在DP过程中对上述的子问题进行修建之后仍不能确保解空间足够小
2.2 强化学习编码
从DP问题中,结合一个实际COP问题可以定义一个强化学习过程,这里有一个关于强化学习的概述
介绍强化学习的作用:
介绍一个基本的过程
2.2.1 State
对于DP问题中不同的阶段,我们可以使用(Q,s_i)作为当前状态的定义,通常状态被embed一种张量作为神经网络的输入,也包括action,最终输出是最优的动作
2.2.2 Action
给定一个DP问题中的state,其中包括一种一对一关系的,$a_i$可以被采用除非$x_i$是有效的,通常可行的动作可以由domain和valid进行判断
2.2.3 Transition
输入当前状态和侗族哦,我们就可以使用DP问题来进行转换就行
2.2.4 Reward
最初的想法是使用DP问题中存在的奖励,但是这样可能会存在没有解的轨迹奖励要高于有解方案的奖励,因此在设计奖励的需要考虑COP问题中存在的两个原则
1, 如果e1比e2更坏,我们需要e1的奖励小于e2的奖励
- 所有找到可行解的轨迹需要比没有找到可行解的轨迹高
UB对应规划问题可能到达的上限,第二个问题强迫智能体去寻找到最佳的可行解,最终的scaling factor 防止最终奖励落入零值周边
2.3 学习方法
DQN
PPO
有一个非常重要的假设,利用生成器得到instance的时候,得到的分布与实际问题中的问题想等,这也是在RL解决其他问题中常见的假设,强化学习的过程是希望学习出不同状态和动作下得到不同的Q,我们的策略往往是采用最大Q值的东西,利用DQN得到Q值的训练过程有
1 | |
展现代码的调用过程
- 这一步仅仅是希望训练出DQN的brain,而没有其他的东西
- 重点在环境生成,以及训练的整个过程
首先确保如何生成一个TSPTW问题
之后生成多个作为训练的集合
同时在每次训练中提高
2.4 网络框架
为了确保框架的通用型和有效性,对于网络框架我们需要确保两件事情
- 对于相同的COP问题,可以有不同的输入尺寸
- 对输入的排列保持不变
为了保证这样的架构我们通常会使用一种Transformer架构,对于TSP问题天然的我们可以采用GAT的方式来实现序列到序列的转换
对于DQN网络中最后一层的输入是不同动作对应的Q- value
2.5 CP Encoding
现在介绍如何将DP过程编码放入Constraint model
| CP | DP | |
|---|---|---|
| variable and domains | X- decision variables,set of the variables,表示动作 | X |
| X-auxiliary variables,表示state | S | |
| D,set of the domain | V | |
| C,set of the constraints | P | |
| O,objective function | 在后面N阶段中的最大值,这里的动态规划方向仅仅和x_a有关 |
2.6 搜索策略
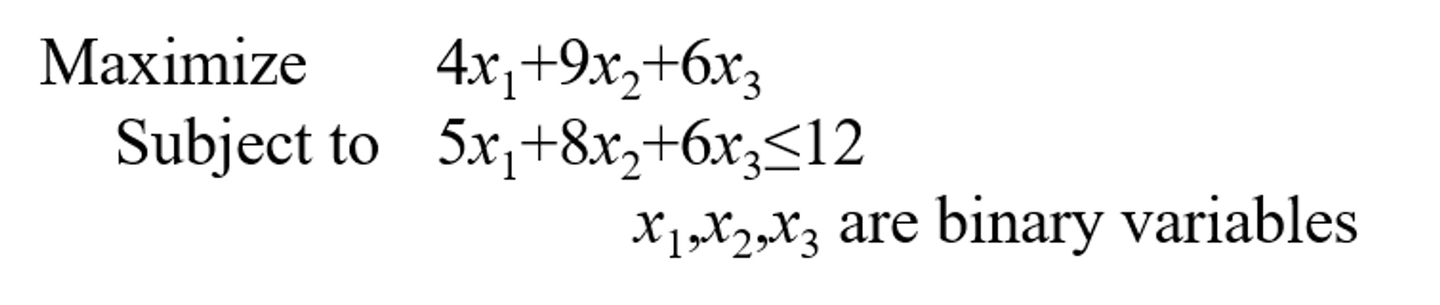
image-20221218155022842
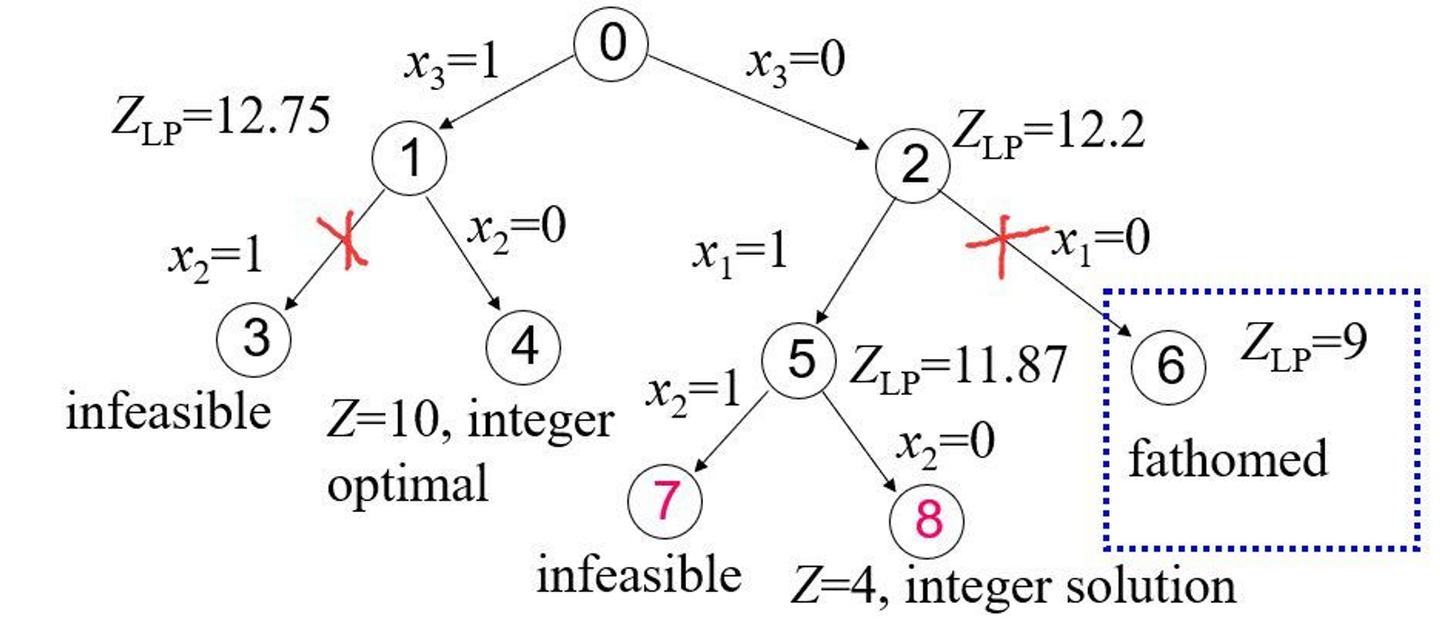
image-20221218155036915
与DP方式相同,我们用此来构建RL的环境(并固定CO问题)来得到动作的输出,框架的统一性是问题的核心,这一部分展示我们如何将学习的模型嵌入到CP搜索中,我们考虑几种常见的搜索方式
- Depth-first branch-and-bound search
- iterative limited discrepancy search
- restart based search
这里仅介绍第一种搜索策略与DQN的结合,DFS确保了当一个可行解找到之后,下一个解需要好与当前的,当遇到没有可行的分支会回溯到之前的分支,由此来确保整个解空间都得到遍历,同时最终得到的解可以被证明是最优的optimal,这个过程中需要非常好的value- selection
在学习之后,DQN的作用是输入当前的状态,以及可行的动作,输入不同动作的最大值,这里可以贪心搜索的方式进行下去,尽管可能不是最优的,需要保证和DP问题中存在的一致性,通常这里会有一些近似变量来作为对DP问题的关键影响,但是这里不是重点
整个过程如下表所示⬇️

image-20221218155108646
3 Experimental result
TSPTW是从传统的TSP问题中得到的,只是给所有的salesman增加一个时间窗的概念,最终规定需要在规定时间内沿着所有的节点走一圈。
Vehicle Routing Problem with Time Windows | OR-Tools | Google Developers

image-20221218155120405
最终证明了结果
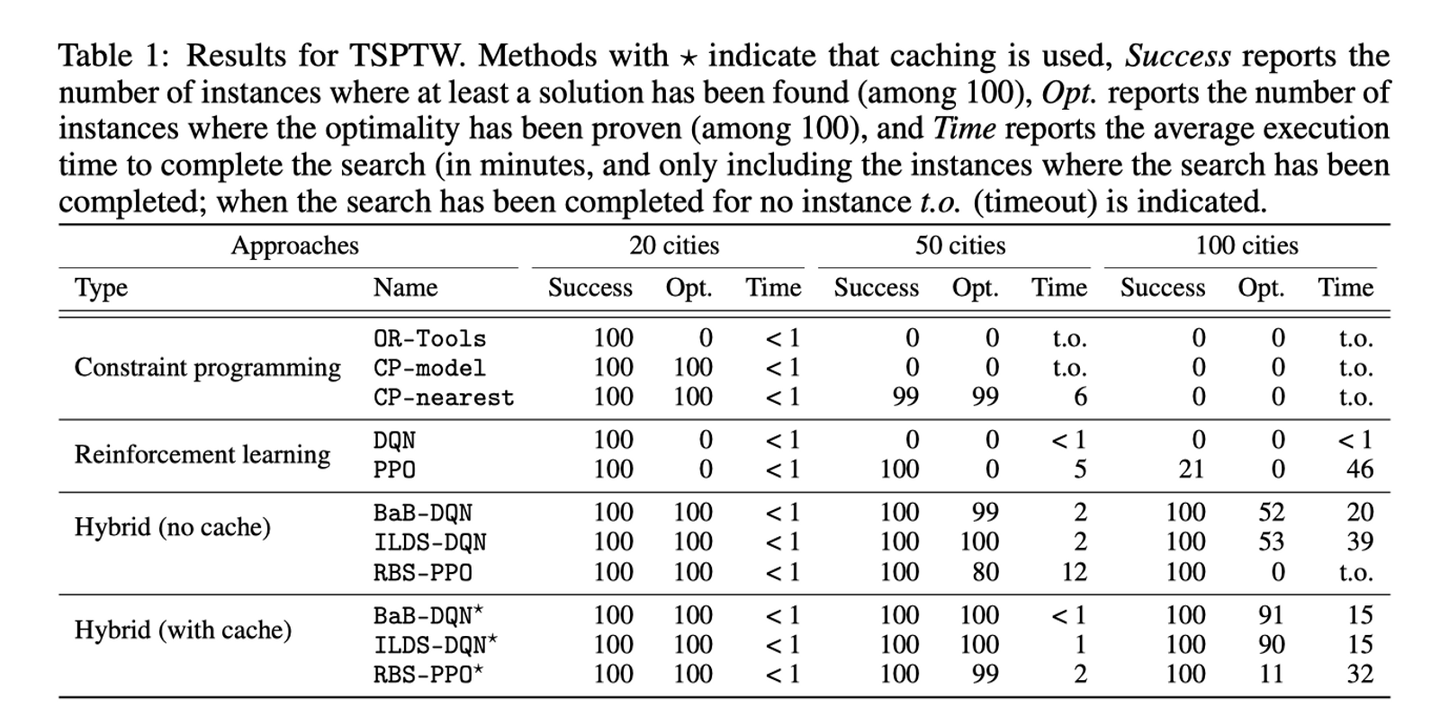
image-20221218155134078
4 Discussion and Limitation
首先本文并不是第一个尝试使用ML来引导优化求解器的分支,但是他们的方法专注于监督学习并且仅限于线性问题,这里本文的共享
- 关注与将COP问题建模成为DP
- 完全利用RL进行训练
同时结合CP问题的完整性,可以更好的求解一系列问题包括非线性约束或者非线性约束函数
同时我们也不需要一些历史数据或者仿真生成器,同时是一种端到端的求解器,并且可以证明求解结果的最优性
5 Conclusion
这些结果表明,该框架可能是解决具有挑战性的组合优化问题的一种有前途的新途径。
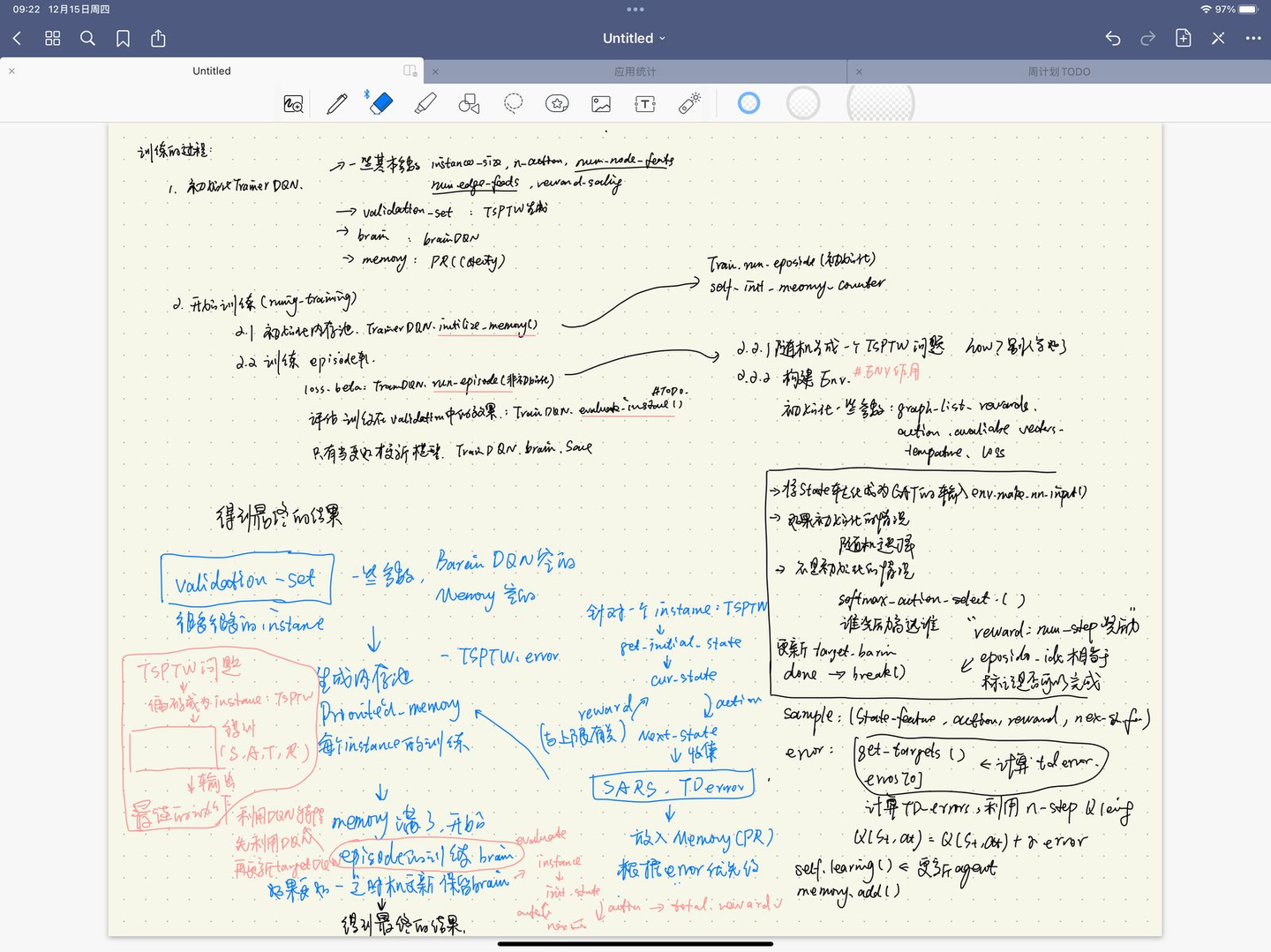
image-20221218155147889