数据结构和算法基础 Vol9

Chenxia

2024-04-29

程序设计

对于图的基础认识和问题描述，进而给出基本的图遍历求解问题的思路

0x01 对于图的基本认识

对于数据结构的存储无非就是“增删改查”，所以对于图（Graph）的认识也可以从这个角度出发。

不过与基本的数组和链表不同的是，数组作为顺序存储、链表作为链接存储更多的是代表计算机存储的一种方式，是更为适合计算理解而对人类不友好的；图作为一个存在日常生活中的数据结构，可以很容易的被人理解，但是往往在计算机存储中存在困难。所以对于图的理解可以从图的本身，以及从图对应的计算机存储方式入手，之后再给出图中一些经典问题。

1.1 图的本身含义

图（Graph）作为一种描述节点（Vertex or node）和节点之间连接的边（Edge）的抽象数据结构，在现实场景中存在很多的应用，比如说具体的交通网络流量、水管布设、计算机网络流量、电路图等等，在抽象中包括人与人之间的社交关系、车与车之间的安全关系等等。同时我们可以节点根据连接边的数量可以增加几个重要的特征：

度（Degree），其中出度表示多少边是从节点发出的，入度表示多少边是从节点接受的；
通路（Path）表示有m+1顶点和m条边组成的序列
首尾相同的通路则为环路（Cycle），同时特殊的环路包括欧拉环路、哈密尔顿环路

根据对节点和边我们可以对图进行简单的分类：

根据边是否有权可以将其分为有权图（Weighted graph）和无权图。这里的区别是图中的边是代表固定的连接和非连接，还是代表一定的数值（比如流量）
根据边是否有方向可以将其划分为有向图（Directed Graph）和无向图（Undirected graph），表示边是表示两端是否连接，还是表示从A点指向B点
根据图中是否包含自环可以将其划分为简单图（Simple Graph）和复杂图，特别的如果其为有向图可以称为有向无环图（DAG，Directed acrylic graph）。

1.2 图的计算机理解

上述主要是从图本身增加了对图的理解，那么我们如何在计算机中表示图呢？考虑到之前的“增删改差”的特点，我们往往希望一种在空间存储上消耗低、在操作时间上开销少的方式来表达Graph这种高级数据结构，因此我们通常会有以下五种基本方法，在评价每个方法的时候要谨记其存储和操作开销，这里我们定义

节点数量为 n
边的数量为 m
D表示节点的度

1.2.1 邻接矩阵（Adjacency Matrix）

很直接的我们会想到点是点，边是边，因此可以通过定义一个点的数组，同时在定义点和点之间边的数组来表示一个图Graph。这样带来的缺点是空间复杂度过高：

新建空间：O($n^2$) 查、增、删：O(1) 新增顶点：O(n) 遍历操作：O($n^2$)

1.2.2 边集数组（Edgeset Array）

由于图中的边已经表示起点和终点，因此如果可以记录所有的边也可以得到对应图的结果

新建空间：O(m) 查询（是否存在某条边）：O(m) 遍历某个点的所有边：O（m）遍历整张图：O（mn）

边集数组适合对于边进行操作的运算，而不适合对于顶点的运算和任何一条边的运算

1.2.3 邻接表（Adjacency Link List）

是一种顺序存储和链式存储结合的存储方式来存储图的节点和边。其中数据结构中数组存放节点的信息，每个数组的元素为链表，用于记录和当前节点链接其他节点的信息。

初始化操作：O(m+n) 查询是否存在边：O（TD（））遍历某个点的所有边：O（TD）遍历整张图：O（n+m）

1.2.4 链式前向星（Linked forward Start）

将上述邻接表中的节点的数组转换成为链表，同时和边集数组结合的方式，可以大幅度的提高建图和遍历效率的额方式，具体的实现方式没看懂～

如果说邻接表是不好写但效率好，邻接矩阵是好写但效率低的话，前向星就是一个相对中庸的数据结构。前向星固然好写，但效率并不高。而在优化为链式前向星后，效率也得到了较大的提升。虽然说，世界上对链式前向星的使用并不是很广泛，但在不愿意写复杂的邻接表的情况下，链式前向星也是一个很优秀的数据结构。 – 百度百科初始化操作：O(m+n) 空间复杂度：O(m+n) 遍历效率:O(m+n)

1.2.5 哈希表

这个比较好理解，主要包括两个哈希表：

第一个哈希表以节点作为key，以下一个终端节点哈希表作为value
终端哈希表中终端阶段为key，边的权重作为 value

图的初始化：O(m+n) 查询是否存在：O(1) 遍历某个点的所有边:O(TD) 遍历整张图：O(m+n)

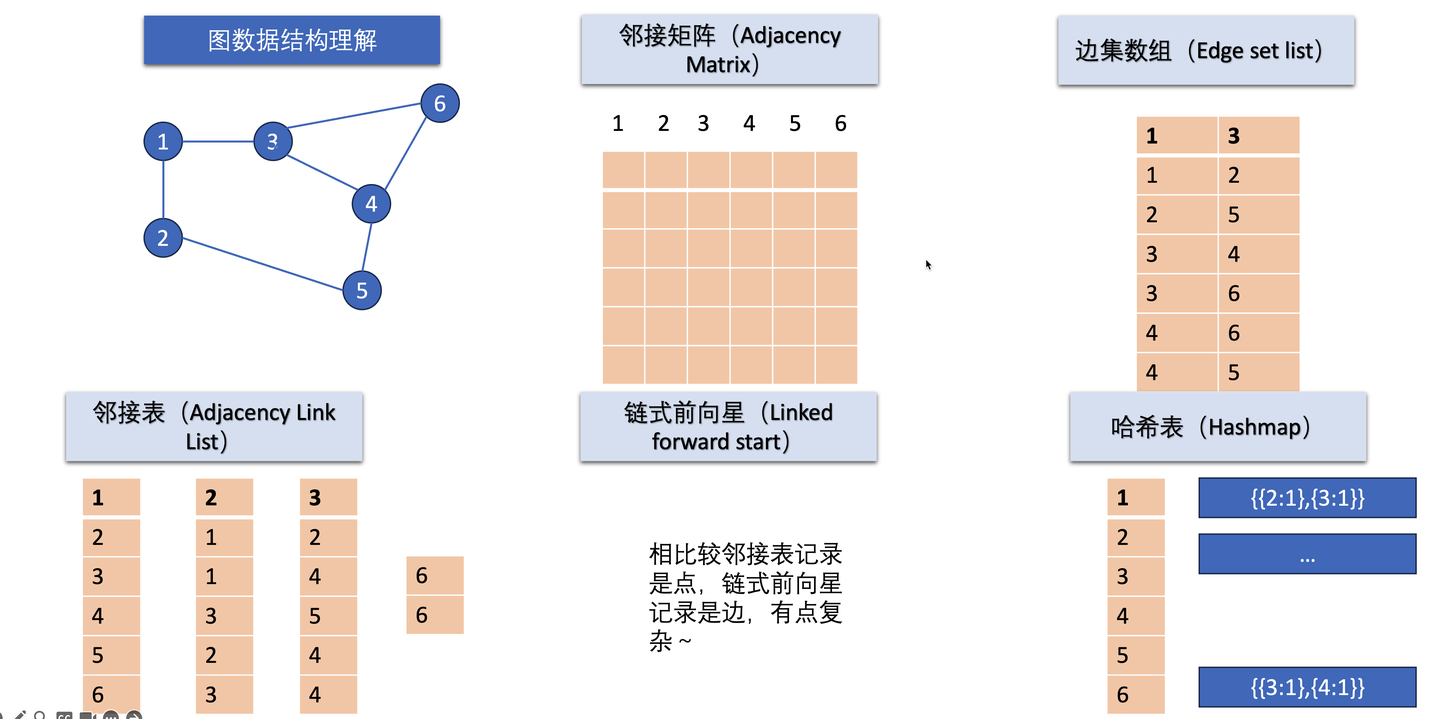
图（Graph）的计算机存储结构

0x02 图的经典问题

既然有图这种数据结构，我们往往会需要什么要的操作呢？这也是我们在现实场景中需要面对的问题，下面将以交通网络为基础，介绍图中的一些典型问题，希望可以在没有实际操作图的基础上，可以对图问题的理解。

首先最基本的是对图的遍历，在通过对节点的遍历的基础上，我们可以使用结合对应的算法来实现最短路径的计算、最小生成树的实现，但是这些依旧是属于点与点之间的问题，我们往往会需要探索图中整体的性质，因此图中的连通性，包括重要的节点和边是需要搜索的对象，在此基础上我们遇到探索对应的网络流问题，来寻找对应的网络流量，

2.1 遍历问题

和其他所有的数据结构一样，我们肯定希望存在一种操作可以获取图中所有的数据。所以最基本的是在知道图的数据结构之后，可以获取所有图的节点。

当你处于世界上任何一个地方，你需要某种方式来知道去其他任何地方的路径

常见的DFS、BFS

2.2 最短路径问题

如果边的权重表示一定的物理含义（运输费用、运输距离等等），我们希望知道节点中A点和B点之间的最短路径的值

在知道如何去一个地方的时候，需要知道那条路径是最低的

常见的有Djikstra算法和Bellman-Ford算法

2.3 生成树问题

我们定义图的树：是包含图G中所有顶点V得树，那么该树就是子图的生成图。由此衍生出最小生成树、次小生成树等问题。

如果一个个体知道点到点之间的路径，从整体的角度我们需要知道遍历所有顶点需要的最小代价，也就是最小生成树

常见的问题方法有prim算法和kruskal算法

2.4 连通图问题

连通指的是图中的点和点之间是否存在链接。但是自然而然的我们会想到图中不同边的属性是不一样的，如果有的边或者节点中断往往会造成网络的瘫痪。

对应交通网络中的主动脉，或者是关键枢纽

2.5 网络流问题

在讨论连通和遍历所有节点的基础上，我们给网络的边增加限制：流量上限，在这种情况下，群体的属性会发生改变，如何讨论边具有流量上限下网络的属性非常有意思

如何计算点与点之间的OD流量的最大流量，以及如何在每条边具有最大流量限制的情况下，计算流量分配来是的整体的费用最少。

常见的概念有最小割、最大流、网络流问题

2.6 二分图问题

讨论是两个二分图之间匹配的问题，属于典型的网络应用

经典的骑手和商家的问题，如果在同一个时间点有n个商家，有n个骑手，如何将骑手分配给商家打车问题，加入同时有n个需求点，有n个出租车，如何将出租车分配给不同的需求点，来是的整体效益最高

常见的算法有匈牙利算法、KM算法

0x03 图的遍历岛屿数量

如果将树看作是自上而下的规则，那么一步一步的我们必然可以得到一个结果，所以我们可以将节点作为状态，将节点的分枝作为动作，这样我们在不同的状态具有不同的状态转移到下一个状态，如果我们需要遍历所有的状态，我们最好的方式是通过搜索的方式（search strategy），这里参考CS188对于搜索问题的解决方式，有两种最基本的方式BFS和DFS。

终点在于：

根据分枝判断下一步的转移方向
能够遍历所有的分枝
记录遍历的过程
到达终点后返回

# node with different actions
path = []
def dfs(node):
    path.append(node.val)
    for action in node.actions:
        dfs(node+action)

所以虽然图看上去形式和树并不一样，我们对于图的遍历方式依旧可以使用DFS或者BFS

T200岛屿数量

首先分析问题是需要寻找所有的岛屿，那么从岛屿的定义中可以达到遍历的条件，也就是找到0的点，遍历的分枝也就是上下左右，同时对于我们寻找的地方我们需要标记为结束。

class Solution:
    def numIslands(self, grid: List[List[str]]) -> int:
        self.m = len(grid)
        self.n = len(grid[0])
        count = 0
        for i in range(self.m):
            for j in range(self.n):
                if grid[i][j] == '1':
                    self.dfs(grid,i,j)
                    count += 1
        return count 

    def dfs(self,grid,i,j):
        # 从grid i 和 j 进行遍历分析
        if i < 0 or i >= self.m or j < 0 or j >= self.n or grid[i][j] == '0':
            return 0
        grid[i][j] = '0'
        self.dfs(grid,i+1,j)
        self.dfs(grid,i-1,j)
        self.dfs(grid,i,j+1)
        self.dfs(grid,i,j-1)

0x04 扫雷问题

这个属于遍历问题的升级版，唯一的区别是岛屿终点的判断并不仅仅是0，而是包括未观测出的地雷的数字。所有从约束编程求解的思路来看，如果一个问题我们求解是NP-hard，但是通常我们验证其正确性只需要P得时间，因此我们可以先得到地图数据的mask，通过点击位置和mask来判断需要展示的区别，进而修改棋盘的状态

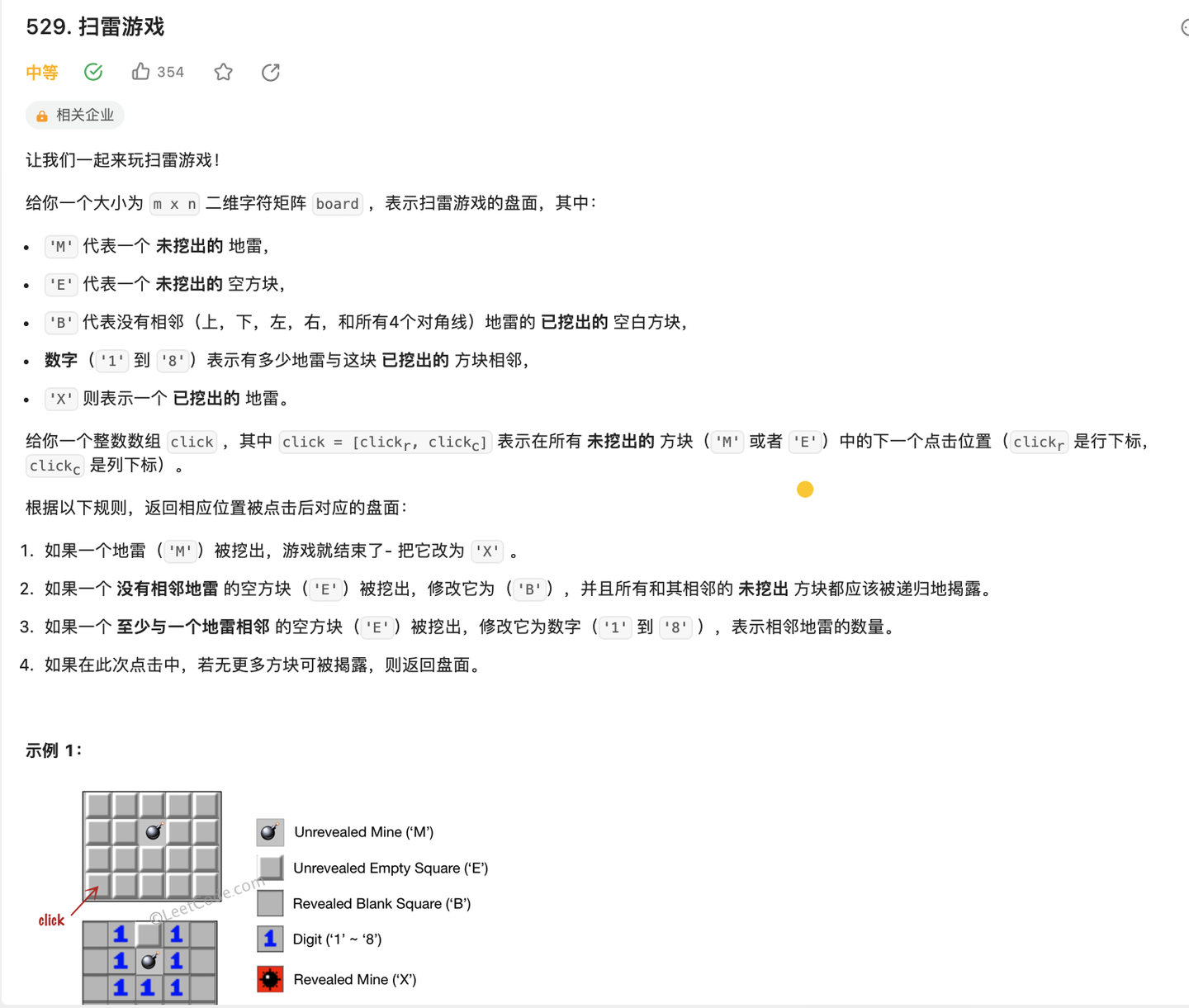
T529 扫雷游戏

class Solution:
    def updateBoard(self, board, click):
        # 将原始棋盘转换成为 recover的形式
        # 同时计算点击下的连通图作为mask
        # 利用mask recovery的合体来实现最终的结果
        self.dirs = [[1,0], [-1,0], [0, 1], [0,-1],
                [1,1], [1,-1], [-1, 1], [-1, -1]]
        self.board = board
        m = len(self.board)
        n = len(self.board[0])
        dp = [[0 for _ in range(n)] for _ in range(m) ]
        for i in range(m):
            for j in range(n):
                if self.board[i][j] == 'M':
                    dp[i][j] = -1
                    for dir in self.dirs:
                        if i+dir[0] >=0 and i+dir[0] < m and j+dir[1] >= 0 and j+dir[1] < n:
                            if dp[i+dir[0]][j+dir[1]] != -1:
                                dp[i+dir[0]][j+dir[1]]+=1   

        # 从click开始进行dfs，三种情况
        # 1. 如果是dp 地雷，将board中的M改为X，返回
        # 2. 如果是dp 数字，将board中的E改为数字，返回
        # 3. 如果是dp 中的0，将board中的E改为B，然后递归的将其相邻的方块改为B
        # loguru.logger.info(dp)
        if dp[click[0]][click[1]] == -1:
            self.board[click[0]][click[1]] = 'X'
            return self.board
        if dp[click[0]][click[1]] > 0:
            self.board[click[0]][click[1]] = str(dp[click[0]][click[1]])
            return self.board
        if dp[click[0]][click[1]] == 0:
            # 说明修改的是E
            self.dfs(dp,click[0],click[1])
            return self.board

    def dfs(self,dp,i,j):
        # loguru.logger.info('dfs')
        if i<0 or i>=len(dp) or j<0 or j>=len(dp[0]):
            # loguru.logger.info('out of range')
            return 
        if dp[i][j] != 0:
            # loguru.logger.info('not zero')
            self.board[i][j] = str(dp[i][j])
            return
        if dp[i][j] == 0 and self.board[i][j] == 'E':
            # loguru.logger.info('zero')
            self.board[i][j] = 'B'
            for dir in self.dirs:
                self.dfs(dp,i+dir[0],j+dir[1])