GEATPY 文档阅读 | 面向过程解决 TSP 问题
各种启发式方法很复杂,当时一般不需要自己手动实现,python中找到GeatPy是个还不错的包,geatpy 是 Python 中的一个进化算法库,专门用于解决复杂的优化问题。它基于遗传算法和进化策略,提供了一个高效、灵活的工具集,用于处理各种优化问题。本文以TSP问题为基础,介绍面向过程,这种最基本也是最直观的想法来介绍库中的基本API。
一、问题描述
TSP问题需要从起始点出发,经过每个点一次,最后要返回原点。要求整个过程经历的路径最短。重点是考虑每个点之间的顺序。
二、问题建模
2.1 启发式建模
我们知道我们输出的结果必然是1xN的向量,那我们的决策变量的大小为N,求解空间为NxN,在这个空间中启发式的生成决策顺序,利用目标函数来决策生成的优劣来寻找最优解。
2.2 整数规划建模
这个领域有一些标准的整数规划建模方法,具体这里不在展开。重要是避免出现子环图的问题
三、启发式方法/GeatPy
按照[1]中介绍的方法对启发式算法的过程进行简介。个人总结启发式算法的思想:
个人愚见 对于NP-Hard问题,既然我们不能自下而上的求解它、但是我们可以快速证明是否为可行解(Feasible- solution)。那我们可以随机生成初始解(1个或者多个),然后计算解对于问题的优劣程度(适应度),之后再通过超现实方式(蚁群、模拟退化、进化算法….)来对解进行重组和重生成,最终收敛得到最终的较优解
所以在进化算法中往往会存在一些基本的概念,包括:
1 | |
启发式算法相比较传统的搜索和优化算法的优势在于:
- 具有天然的并行性
- 进化算法使用的是概率转换规则,而不是非确定转化规则
- 进化算法使用的是目标函数和适应度条件即可影响搜索方向
其中重要的地方在于
- 针对特定问题的决策变量确定,也就是编码
- 适应度函数的确定
- 选择 selection、重组Reorganization和变异Variation算子
3.1 变量编码[2] Encoding
和传统的搜索问题的方式并不一样,启发式算法的搜索问题是针对求解空间的,那么需要将原始问题转换成为一个$f(x)$, 其中$x$的值域辨识搜索空间,也就是编码空间(有点绕口),编码过程中需要的基本原则
- 完备性:问题所有可能的解可以fully map到编码空间
- 可靠性:编码空间需要对应一个潜在解
- 非冗余性:一一对应
编码的方式对启发式搜索过程十分重要,常见的方式包括:
- 一维或二维度的数据列
- 二进制数据列的字符串
- 简单映射编码
- 多重映射编码
- 排列编码
- 树编码等等
3.2 适应度编码[3]
适应度表示的是生成解和问题之间的匹配程度,它的计算是使用遗传算法的关键要素,制定了后续选择、变异和重组的搜索方向,直接关系到搜索效率和最终求解的质量。
适应度的常见来源使用规划模型的目标函数作为适应度,其需要遵循的规则通常有:
- 遵循单调原则
- 适当的变换来影响收敛速度。比如线性变换、指数变换、幂指数变换、截断处理、罚函数、基于等级的适应度分配计算。
3.3 选择 Selection[4]
选择分为两个阶段,第一个阶段是筛选现有解来生成下一个过程的解;第二个阶段是生成的下一个过程的解再进过一次“环境选择”
第一阶段,这里是选择参与进化操作的解。为了保证“探索-利用”的均衡。一部份是适应度较高的解、另一种是随机筛选的个体。没有被选中的解不会进入变异、重组的进化操作中。
第二阶段,个体经过进化操作之后子代保留到下一代的过程。常见的方案包括全局重插入(Global reinsertion)和本地重插入(Local reinsertion)
在选择的过程中我们需要考虑如何选择才是最合理的?这里的评价标准主要包括:最优解选择概率(selective pressure)、选择偏差(bias)、多样性损失(loss of diversity)、重复选择上限(spread)、选择强度(selection intensity)、选择方差(selection variance)
经典的选择算子包括:
- 轮盘赌操作(roulette wheel selection),有回放的随机抽样选择
- 随机抽样选择(stochastic universal sampling)
- 锦标赛选择(tournament selection),随机选择一定规模的解来找到最优
- 截断选择(truncation selection)
- 本地搜索(local selection)
- 基变量选择
- 一对一生存竞争选择
3.4 重组[5] Recreation
重组指的是通过结合交配群体的遗传信息来产生新的个体。通常其和问题编码的二进制编码、实值编码、排列编码、树编码方式有关,需要根据不同的编码来确定不同的重组算法。
重组包括重组片段概率和重组概率:
- 重组片段概率,操作的片段长度
- 重组概率,两个是否发生重组的概率
3.5 变异[6] Mutation
变异指的是通过改变原始解来生成新解的过程。参考对于自然界的观察,这个过程的基本原则是保持多样性,来避免陷入局部最优解的风险。以下给出常见的变异算法:
- 二进制染色变异,在二进制中选择某些变异为0,某些变异为1
- 实值染色变异
- 均匀变异
- 高斯变异
- 多项式变异
- 差分变异
- 整数值变异
- 采用实值变异之后四舍五入
- 互换突变,在组合优化问题中染色体中的每个值都是独一无二的,因此常见的采用互换操作的方式来进行突变
四、GeatPy入门
GeatPy(Genetic and Evolutionary Algorithm Toolbox)是一个为Python设计的高性能进化算法框架和工具箱,能够快速解决单目标、多目标、多目标和组合优化问题。
4.1 概述
GeatPy开发的角度主要四个抽象类,Problem、Population、PsyPopulation、Algorithm:
- 问题类Problem,定义问题的名称(name)、优化目标维度(M)、决策变量维度(Dim)、决策变量范围(ranges)、决策变量边界(borders)、等式方向(maxormins)、变量类型(varTypes)、目标函数(aimFunc())、计算或读取目标函数参考值(calReferObjV())
- 寻解种群(Population、PsyPopulation),包括染色体(Chrom)、编码方式(Encoding)、译码矩阵(Field)
- 算法Algorithm,求解问题相关,包括之前抽象的各种算子
4.2 数据结构
种群染色体chrom:默认一行chrom对应一条染色体,因此维度为:
基因表现型Phen:对于染色体解码之后的表达的变量,在实值编码下两者是一致的
目标函数值ObjV:单目标函数
个体适应度FitnV:最小适应度为0,维度为
违反约束程度CV: 存储每个种群违反约束条件的程度,维度为.Note: GeatPy处理约束的方式包括罚函数法和可行性法则
4.3 快速入门 Get start
- 直接使用工具箱提供的库函数,通过编写脚本来实现进化算法并且求解问题
- 使用GeatPy提供的面向对象的算法框架,使用内置的算法模版求解问题
- 使用GeatPy提供的面向对象的算法框架,使用自定义进化算法实现进化算法并且求解问题
五、实现TSP问题(原始方法)
5.1 初始化问题
1 | |

TSP问题
5.2 定义目标函数
记得目标函数的输入是,输出是
1 | |
5.3 定义种群属性
需要确定种群的:
- 编码方式(决策变量variable和染色体Chromosome)之间的关系
- 确定染色体的变化范围,FieldD,具体包括变量类型、变量上下限、上下限等号
- 种群数量
因为TSP问题属于组合优化问题,因此可以采用排序编码,这样情况下“染色体”和“决策变量”是一直的,因此不需要相互转换
1 | |
5.4 定义进化过程
进化过程主要需要确定
- 选择算子,这个一般是通用的;可以参考API文档来看
- 交叉算子,这个需要根据具体的编码方式来确定;可以参考API文档来看
- 变异算子,这个也需要根据具体的编码方式来确定;可以参考API文档来看
这里有一个坑就是算子的实现GeatPy也在不断更新,这里采用ea.crtpc和ea.Mutpp来构造
1 | |
5.5 求解过程
1 | |
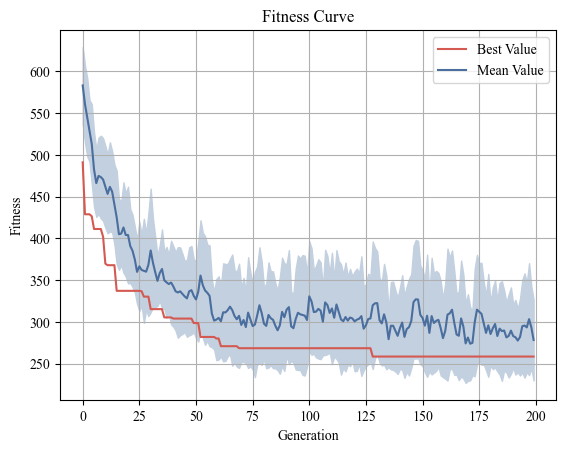
TSP求解过程
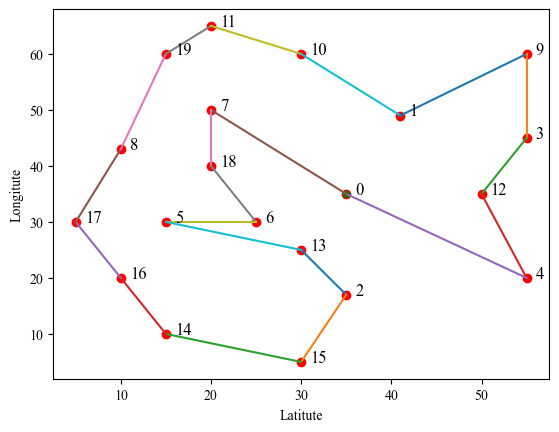
结果示意图