面试经验 Vol2 ｜ 损失函数和评价指标总结

Mitchell 在《机器学习》中对其的定义是：

一个计算机程序被认为能够从经验 E 中学习,去完成任务 T,达到性能度量 P,当且仅当,通过经验 E 的学习,其在任务 T 上的性能度量 P 得到了提升。

假设我们有一个模型 $f(x;θ)$,其中 x 是输入,θ 是模型的参数。给定一组训练数据 $D={(x_i,y_i)}_{i=1}^N$,其中 $x_i$是输入,$y_i$是对应的目标输出。我们的目标是找到一组参数 θ,使得模型 f(x;θ) 在任务 T 上的性能度量 P 最大化。

这里,损失函数 L(f(x;θ),y) 的作用就是衡量模型的预测输出 f(x;θ) 与真实目标输出 y 之间的差异。我们希望通过最小化损失函数,来找到最优的模型参数 θ。因此,机器学习的任务可以表示为一个优化问题:

$$ min_\theta \frac{1}{N} L(f(x_i;\theta),y_i) $$

通过最小化训练数据上的平均损失,我们得到了一组最优参数 θ,使得模型 $f(x;\theta)$在任务 $T$上的性能度量 P 得到提升,从而实现了从经验 E 中学习的目标。

在学习链路的整个过程中，数据（E）、模型（计算机程序）、度量（L）、训练（T） 都是非常重要的部分，本文主要针对学习过程中针对不同的任务设计不同的损失函数，来实现模型效果的最优化。

0x00 如何设计损失函数

1.1 ERM 输出～标签

如果把数据看作是历史观察的经验，那么经验风险就是模型在训练数据上的平均误差：

$$ R_{erm} = \frac{1}{N}\Sigma L(f(x_i),y_i) $$

1.2 SRM 模型本身

由于模拟复杂度和问题复杂度之间不匹配会造成《欠拟合或过拟合》的问题，因此通过对模型的复杂度进行限制有有效的避免过拟合

$$ R_{srm} = R_{erm}+\lambda \Omega(f) $$

初次之外，我们可能需要根据不同的任务来区分不同的损失函数设计方式，比如：

1. GAN 的损失函数设计，将生成器看作负样本，将真实样本看作正样本，训练过程
2. SVM 的损失函数设计，利用最大间隔来区分正负样本
3. 交叉熵或 KL 散度，利用信息论来衡量模型预测概率和真实概率分布的差异
4. 排序学习损失函数设计，包括 list wise、Pair wise、List wise 等方式计算

分类	Cross entropy	回归	Square loss	LTR	pairwise CE
	hinge loss		absolute loss		pairwise Hinge
	Focal loss		Huber loss		pairwise Square
	weighted CE		Log loss		lambdaRANK loss
					ListNet loss
对比	infoNCE	多任	Linear weighted	多标	soft margin
学习	Triplet	务学	Mean squared	签学	ranking
	NCE	习	uncertain loss	习
	CPC		gradient norm

初次之外还包括很多其他的任务，比如分类、回归、学习排序、搜推广、强化学习、生成学习、对比学习、度量学习、多任务学习、异常检测损失、few-shot 学习、零样本学习、多标签学习、非监督学习损失、半监督学习损失、持续学习损失函数、因果推断损失等等。

0x01 分类损失函数

1.1 Cross Entropy 损失

利用0-1 分布可以推导出对应的损失函数，注意这里的y_hat 是概率，y是 0-1 标签

$$ L(y,y_{hat}) =\Sigma ylog(y_{hat})+(1-y)log(1-y_{hat})) $$

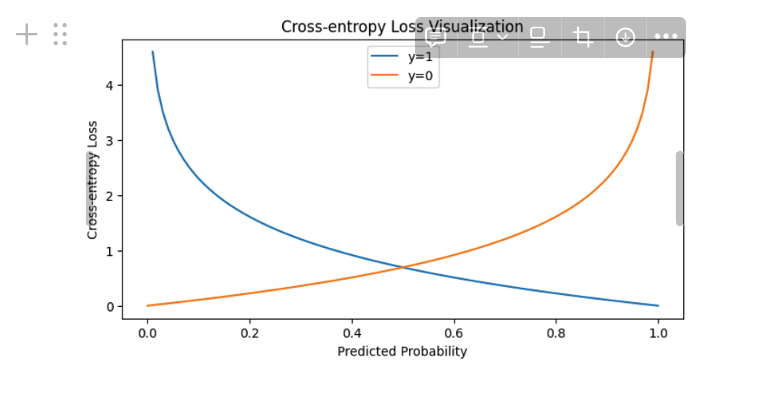
1.2 KL散度

KL 散度 = 交叉熵 - 信息熵，用于策略两个概率分布差异的方法，其数学表示为；注意通过这个可以看出两者具有非负性、非对称性。

$$ KL(P||Q) = \Sigma_xP(x)\frac{P(x)}{Q(x)} $$

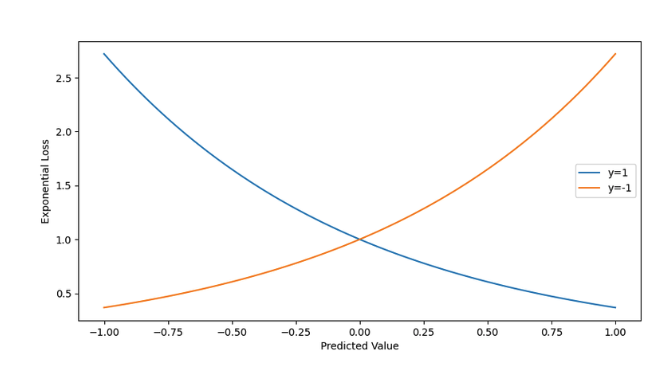
1.3 指数损失

同号时两者的损失较小，当两者sign 不一致后导致惩罚急剧增大

$$ L = \Sigma exp(-y_if(x_i)) $$

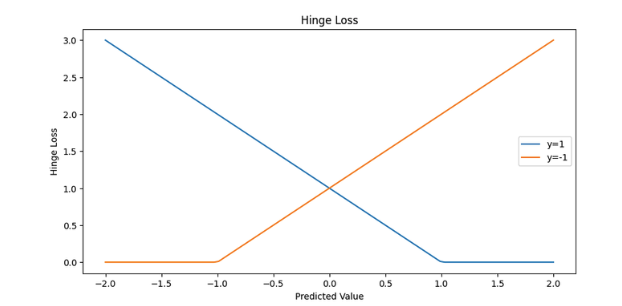
1.4 Hinge los

确定性较强时损失为 0，否则损失不为 0

1. 间隔最大化：Hinge loss 通过惩罚位于正确分类一边但距离决策边界太近的点，以及位于错误分类一边的点，从而鼓励模型找到一个能够最大化正负样本间隔的决策边界。
2. 对正确分类的容忍度：如果一个样本被正确分类，并且其预测值与实际标签的乘积大于1（即，它们之间的间隔超过了1），那么这个样本对损失函数的贡献为0。这意味着模型不会因为正确分类的样本而受到惩罚，只要这些样本距离决策边界有足够的间隔。
3. 对错误分类的惩罚：对于错误分类的样本（即，预测值与实际标签的乘积小于1），损失值随着分类错误的程度增加而增加。这促使模型减少这些错误。

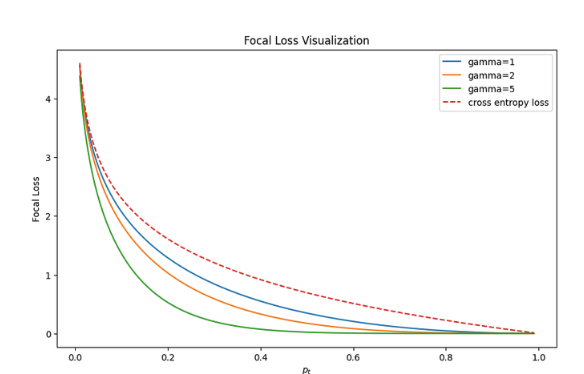
1.5 Focal loss

通常用于解决分类任务中的类别不平衡和难易样本的问题。它是一种针对二分类问题设计的损失函数，旨在减轻易分类样本对模型训练的影响，使得模型更加关注难分类样本，从而提高整体分类性能。因此，Focal Loss属于分类任务中的损失函数。

$$ FL(p_t )=−α_t (1−p_t )^γ log(p_t ) $$

import torch
import torch.nn as nn
import torch.nn.functional as F

class FocalLoss(nn.Module):
    def __init__(self, gamma=2, weight=None, reduction='mean'):
        super(FocalLoss, self).__init__()
        self.gamma = gamma
        self.weight = weight
        self.reduction = reduction
        
    def forward(self, input, target):
        # 计算交叉熵
        ce_loss = F.cross_entropy(input, target, reduction='none')
        
        # 计算pt
        pt = torch.exp(-ce_loss)
        
        # 计算focal loss
        focal_loss = ((1-pt)**self.gamma * ce_loss).mean()
        
        return focal_loss

0x02 回归损失函数

2.1 MSE 均方差损失函数

用于衡量样本真实值和预测值之间的差距，利用概率可以推导出背后的公式

2.2 RMSE 均方根误差损失函数

保证与样本量纲保持一致

2.3 MAE 绝对值损失

0x03 对比学习（contrastive learning）中的损失函数

对比学习（Contrastive Learning）综述

这里总结一下对比学习的基本思想，主要是通过度量两者分布的距离，保证同类别度量尽可能小，不同类型之间的距离尽可能的大

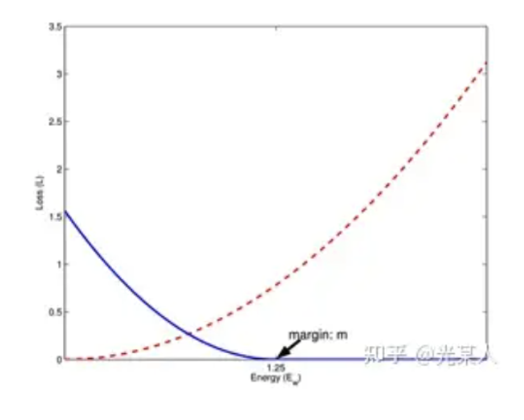
3.1 contrastive loss

对比损失中其中最困难的应该是如何在无标签数据中定义标签来进行学习，其中 d 代表的是(x1,x2)之间的样本距离，其中 y 表示两者是否为同类型的样本，类比弹簧势能 的定义：

1. 对于模型预测为同类别，1，但是样本实际的距离越远，两者之间的损失越大
2. 对于模型预测为非同类，0，但是样本实际的距离越远，两者的损失函数越小；至少保证在一定 margin 外不会出现 0 的情况

对比损失属于 Pair wise 的一种，在通常的情况下并不需要计算所有样本下的损失，而是计算正样本和负样本之间的距离可以作为方式，或者增加一些随机样本、负采样、软采样的方式。

$CL = \frac{1}{2N}\Sigma [y_i ⋅d^2 +(1−y_i )⋅max(margin−d,0)^2 ]$

3.2 Triplet los 三元组损失

但是在实际的训练过程中，我们并不确定所有的样本都可以计算，同时假设所有的样本无限拉近可能会导致过拟合的风险。因此希望通过对比的方式将三元组分为（x 正，x 负，x）;也就是将数据集划分为：Anchor、positive、negative

$$ L= max(d(x^+,x)-d(x^-,x)+\alpha,0) $$

FaceNet: A Unified Embedding for Face Recognition and Clustering

在搜索推荐场景中：

1. anchor：用户当前搜索查询的浏览记录
2. postive：用户点击或者互动过的相关商品和内容
3. negative：用户未点击或互动的不相关的商品

3.3 NCE loss

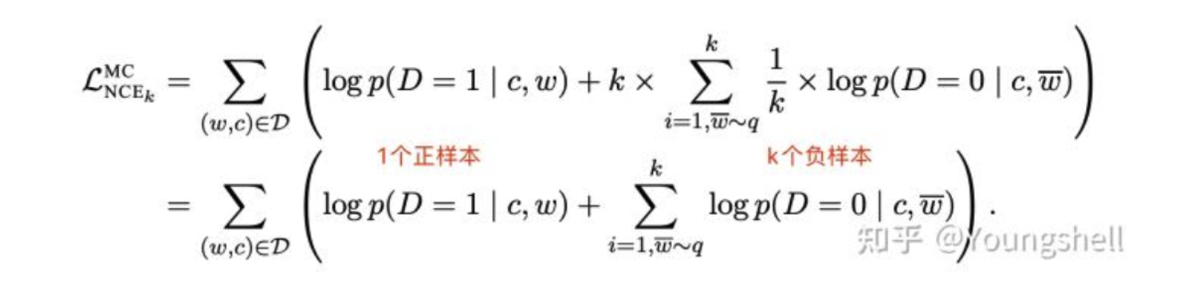
3.4 Info NCE loss

3.5 Center loss

A Discriminative Feature Learning Approach for Deep Face Recognition

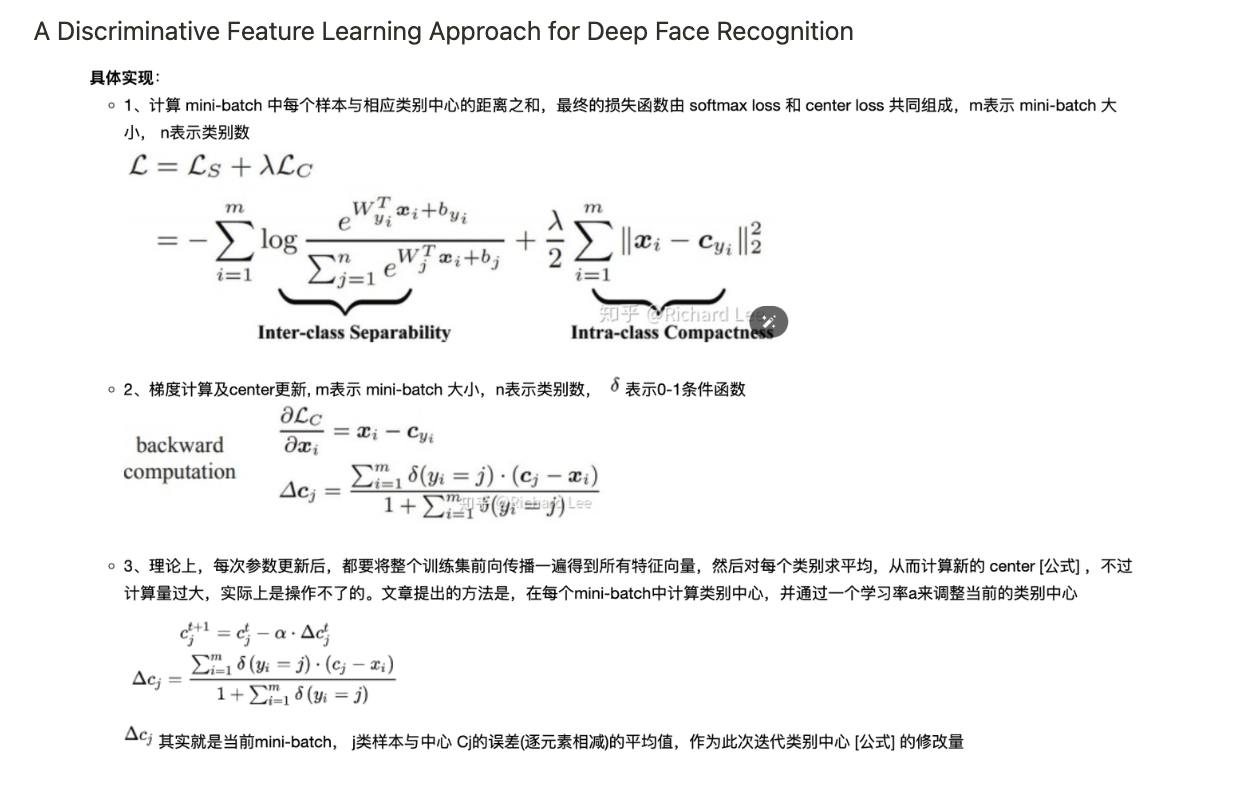
3.6 Circle loss

0x04 排序学习（learning to rank）中的损失函数

LTR(Learning to Rank)概述

了解排序问题首先需要明确目的，比如在搜索问题中，最关心的是返回 N 个样本的相关顺序关系，而不是每个样本的预测值最准确，属于 ranking 问题（另一类是 rate 问题）

对于训练样本的标注主要包括以下两种：

1. 人工标注，针对搜索结果进行不同等级的划分
2. 历史数据，通过搜索历史来获取对应的标注，对应这种观察数据存在选择偏差

根据 Point wise、Pair wise、List wise，

1. Pointwise: Subset Ranking, McRank, Prank, OC SVM
2. Pairwise: Ranking SVM, RankBoost, RankNet, GBRank, IR SVM, Lambda Rank, LambdaMart
3. Listwise: ListNet, ListMLE, AdaRank, SVM MAP, Soft Rank

0x05 生成学习（Generative）中的损失函数

https://github.com/hindupuravinash/the-gan-zoo

0x06 多任务学习（Multi-task learning）中的损失函数

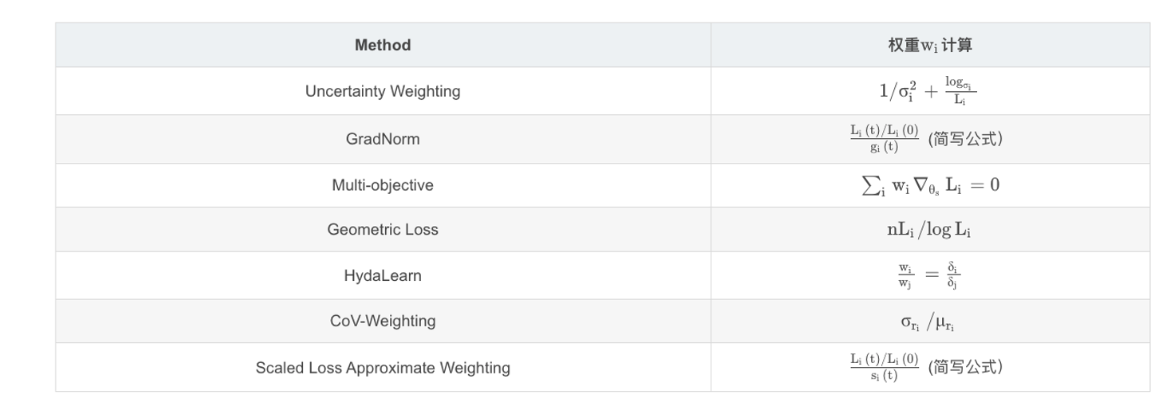
1. uncertainty weighting 不确定性
2. Grad normalization 梯度均衡
3. Multi-objective optimization
4. Geometric loss
5. HydaLearn 存在的问题
6. Cov - weighting 动态计算
7. Scaled loss approximate weighting