CS229 机器学习 Vol10 ｜ 课后作业 1

CS229的homework之前一直没有写，趁这个寒假结束掉它！如有错误欢迎指正！

0x01 Gradients and Hessians：求导和海森矩阵

1.1 定义回顾

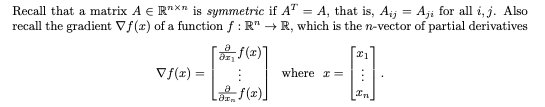
多元函数一阶导

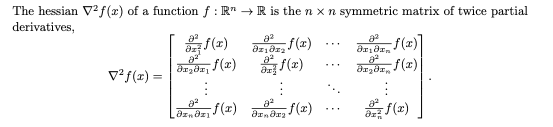
多元函数二阶导

Symmetric: 对称矩阵

1.2 问题

问题

1.3 解答

(1)∇𝑓(𝑥)=𝐴𝑥+𝑏

(2)∇𝑓(𝑥)=𝑔′(ℎ(𝑥))∇ℎ(𝑥)

(3)∇2𝑓(𝑥)=𝐴𝑇=𝐴

(4)∇2𝑓(𝑥)=𝑔″(𝑎𝑇𝑥)𝑎𝑇𝑎

0x02 Positive definite matrices : 正定矩阵

2.1 定义回顾

positive semi-definite(PSD): 半正定矩阵

positive definite: 正定矩阵，eg：单位阵

正定矩阵定义

Null-space: 核，表示一个算子的零空间是方程$AV=0$的所有解$v$的集合

Rank: 矩阵A的列秩是A线性无关的纵列的极大数目；可以用于计算线性方程组解的树木、也可以用来确定线性系统是否为可控制的、可观察的

2.2 问题

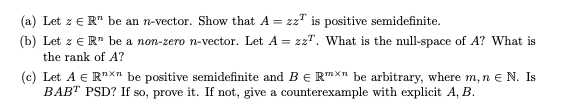
2.2 问题

2.3 解答

两边同时乘$x^T$

可以化简为

因为$Rank(z) \leq 1$,但是z非零;结合$Null(A)=Null(z)$

结合A的PSD特点可以证明，略

0x03 Eigenvectors，eigenvalues，spectral theorem：特征向量、特征值、谱定理

3.1 定义回顾

Eigenvectors & Eigenvalues：特征值和特征向量

求解$p_A(\lambda)=det(\lambda I-A)$或者$Ax=\lambda x$之间的关系

Diagonal matrix：对角矩阵，可以用$det(d1,d2,…)$表示

Orthogonal：正交矩阵

Spectral theorem：谱定理

3.2 问题

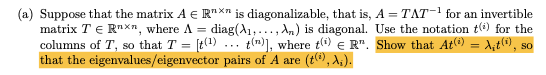
image-20230109110250716

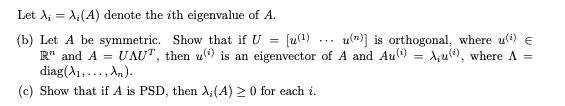
image-20230109110258767

3.3 解读

两边同乘逆

又$\Lambda=diag(\lambda_1,…,\lambda_n)$

所以特征值对应的向量为$(\lambda_i,t^{(i)})$

因为A是对称矩阵，U为正交矩阵，同时

所以同上

根据谱定理可以得到

因此大于等于0