CS229 机器学习 vol11 | 课后作业 2
Problem set00 是关于线性代数和多元微积分学的基本知识,Problem set 01主要是监督学习。作业要求最好使用LaTex进行编写,同时需要将library保存到environment.yml文件中,并保证run.py脚本可以正常运行。
0x01 线性分类(逻辑回归和广义线性模型)
1.1 问题回顾
Linear classifiers ( logistic regression and GDA)
在本次作业中将回顾之前的概率线性分类器,
- 判别线性分类 (discriminative linear classifier) :逻辑回归
- 生成线性分类 (generative linear classifier):高斯判别模型
两者均可以将一个数据集分成两类,但是基于不同的假设,本次问题的目的是找到两者的相同点和差异。
1.2 实际问题
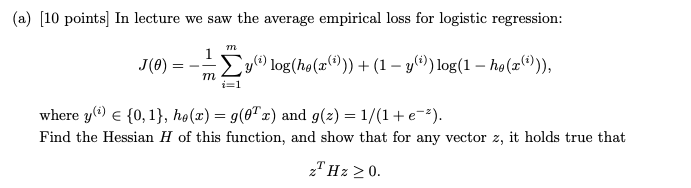
问题1-(a)
注意Hessian矩阵为PSD,则说明损失函数是凸(convex)的,也就是存在极值点
𝑝(𝑦|𝑥,𝑡ℎ𝑒𝑡𝑎)=𝑝(𝑦,𝑥,𝑡ℎ𝑒𝑡𝑎)/𝑝(𝑥,𝑡ℎ𝑒𝑡𝑎)=𝑝(𝑥,𝑡ℎ𝑒𝑡𝑎|𝑦)𝑝(𝑦)/𝑝(𝑥,𝑡ℎ𝑒𝑡𝑎)

1-b

1-c

1-c(2)

1-d
1.3 问题求解
由于公式较多,只能给出思路
(1) 展开求导就能发现是大于0
(2)coding就完事了,numpy的MATLAB的矩阵计算方式
(3)GDA按照贝叶斯展开就行了
(4) 发现是相同的
(5)(6)(7)(8)是一些可视化的东西
0x02 不完整、只有正标签:Incomplete,Positive- only labels
2.1 问题回顾
假设在我们没有得到完整的标签的情况下的,只能确定性得到部分的正样本,而不能得到其他样本的标签。也就是所有负样本和剩余的正样本是没有标签的。
这道题的问题设置更像是一种引导,如何理解这种情况下如何构建模型
2.2 问题

2-a
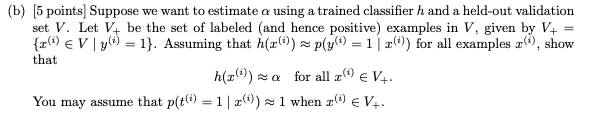
2-b
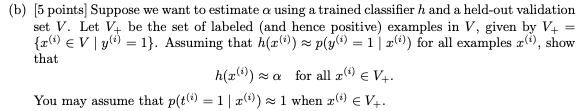
2-c
后续是那个coding problem
2.3 问题解答
(1) 简单随机样本抽样
0x03 泊松分布的拟合
重新回归GLM中的三个基本假设:

GLM-assumption

GLM-assumption02
本重新认识到:
- 第一个assumption给出了y的分布!这可以用来计算似然函数
- 第二个assumption给出如何确定hypothesis,也就是模型
- 第三个assumption似乎是人们设计好的,这样我们才能对一些线性模型做假设
0x04 广义线性模型的convex相关的研究
太理论了看不下去~
0x05 加权线性回归
除了 利用gradient descent求解,也可以使用normal equation来进行参数的求解;非常的奇妙!
注意这部分和后面的attention有关系
后面的公式太多了不想打,
0x06 感悟
动手才能发现学习的问题所在,动手才能知道代码应该如何实践!
对于现实世界的抽象可以帮助我们进一步学习和研究,虽然矩阵的定义很简单,但是只有在这个抽象定义的基础上才能发展出线性代数这门学科,才能用此解决问题。