数据结构和算法基础 vol8

重新回顾二分查找必要的细节

0x01 算法想法

二分查找（Binary search algorithm），是在数组章节第一次体会到算法精神的算法。其基本思想是：先确定待查元素的范围，之后以某种方式缩小范围，直到到达某种条件为支。很while

其基本的算法思想是“减而治之”，和分而治之类似，但是更加的巧妙的是在于如何减小问题的规模或者排除问题。二分查找算法流程为：

1. 每次查找从数组的中间元素开始，如果中奖元素正好是要查找的元素，则搜索过程结束
2. 如果中间元素大于或者小于特定元素，那么选择对应的左边或者右边查找
3. 如果为空则说明找不到

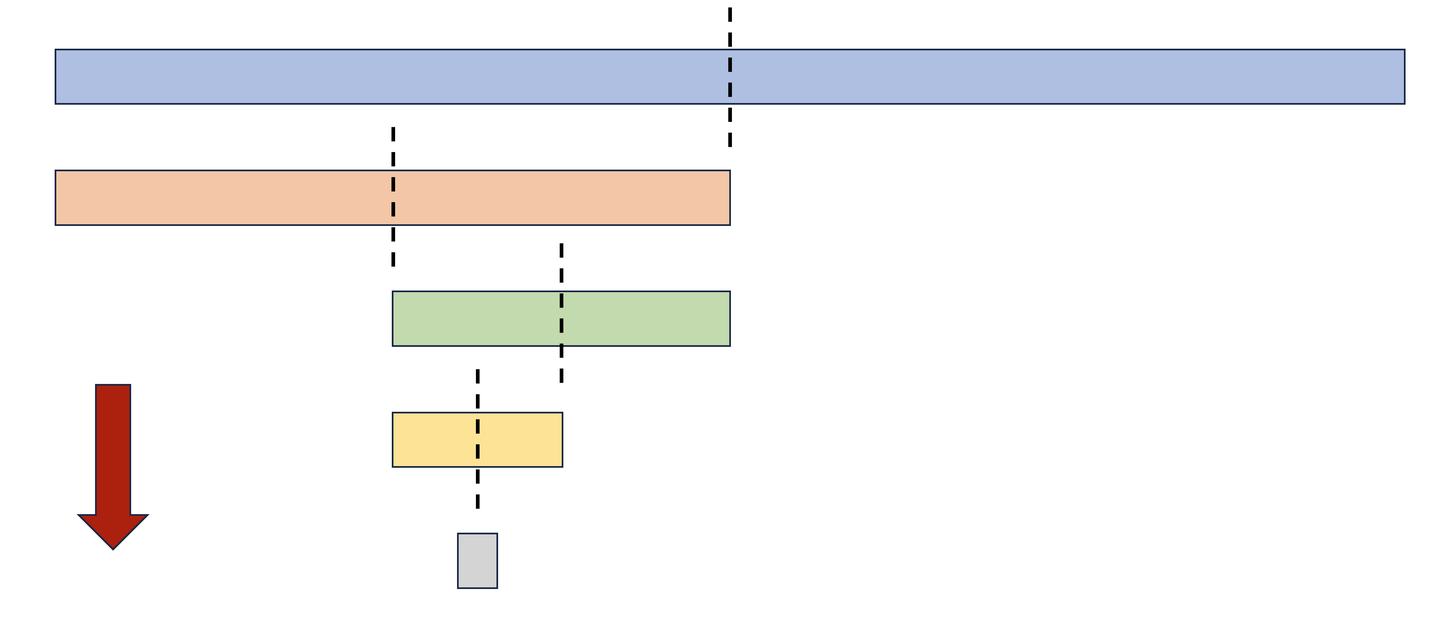
二分查找过程

0x02 魔鬼细节

想法并不困难，以最基本的方式从一个升序的数组中查找某一元素：

# arr = [1,2,3,4,5,6,7,8]
# target = 3
left = 0
right = len(arr)-1
while left<=right:
  mid = left+(right-left)//2
  if arr[mid]>target:
    right = mid-1
  if arr[mid]<target:
    left = mid+1
  if arr[mid]==target:
    return mid
  return None

同样也可以这样写

# arr = [1,2,3,4,5,6,7,8]
# target = 3
left = 0
right = len(arr)
while left<right:
  mid = left+(right-left)//2
  if arr[mid]>target:
    right = mid
  if arr[mid]<target:
    left = mid+1
  if arr[mid]==target:
    return mid
  return None

这里魔鬼的地方在于

1. 选择的初始状态的选择，left还是right
2. 以及最终条件的判断，left小于right 还是 left 小于等于 right
3. 以及每一步比较之后的选择，left = mid-1 还是 left = mid

其实如果刷题的话可以发现二分查找主要分为三种搜索：

1. 搜索给定值的下标
2. 搜索最左边的值
3. 搜索最右边的值（可以转换为第二种）

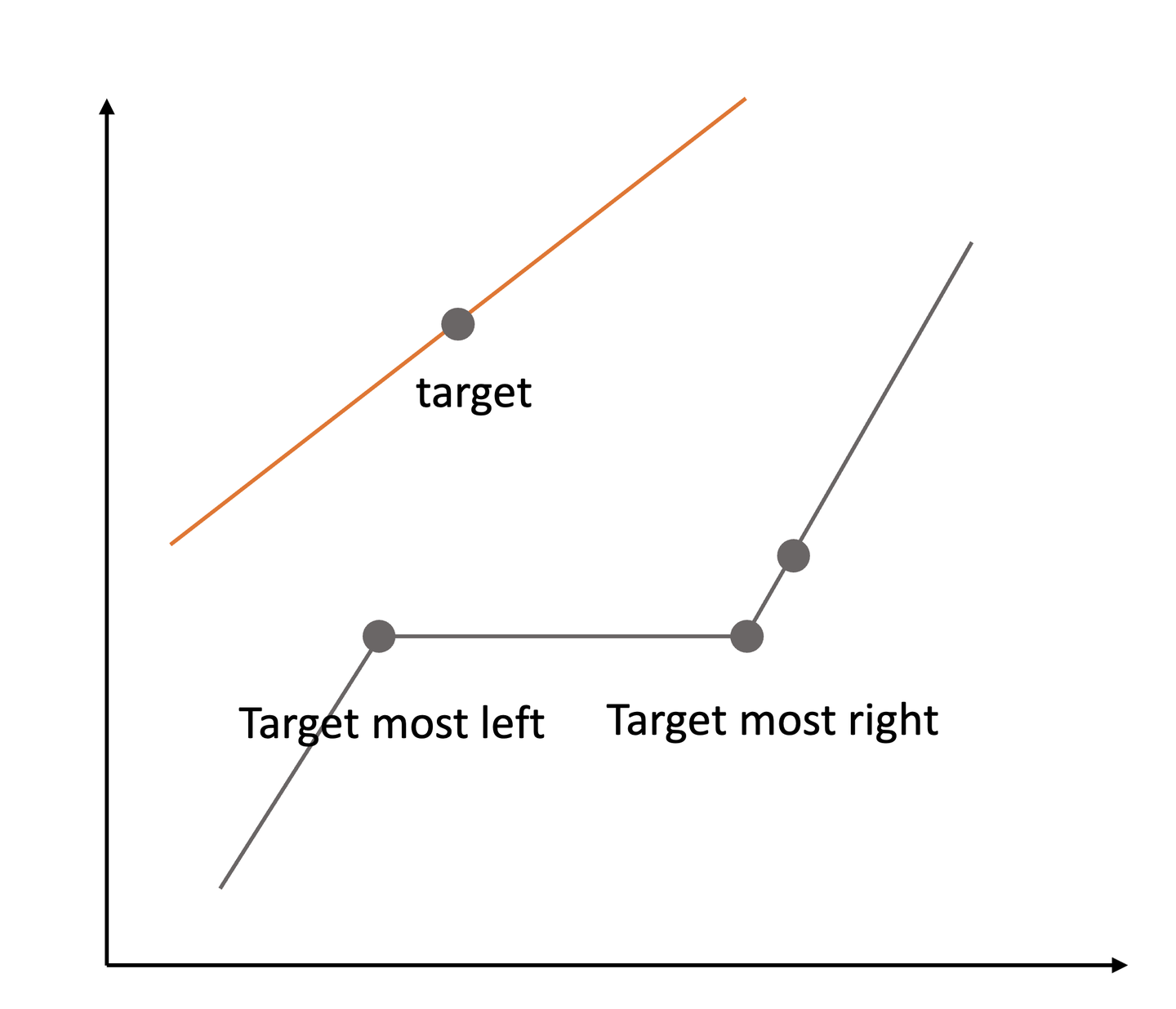
常见搜索

在二分查找缩小空间的方式中，我们唯一能做到的只有排除我们确定没有的空间。比如对于第一类寻找目标值，如果arr[mid]确定小于target，我们相信一定不在这个区间，那么我们可以设计为left = mid+1，因为包含mid的区间我们知道一定不存在。而对于第二类寻找最左边的值，如果arr[mid]大于等于target我们也不能确定是否一定在mid-1的区间中，因此我们这个时候需要选择开区间，且设置right = mid而不是right=mid-1

0x03 反思

搜索解空间其实只有两种，一种是确定我们剩下的，另外一种是排除不存在的。