CS285 深度强化学习 Vol6 ｜ Actor Critic

主要介绍演员评论家过程,从最基础的Policy Gradient中剖析如何拟合Policy Evaluation的部分，并推导得到Actor- Critic算法。可以看出从之前直观的Policy，到利用state- value或者action- state- value进行近似。这个过程中采样结果与理论推导的权衡贯穿理论推导过程。在这个基础上也会引来下一节Lecture07关于value function方法。同时突然有个新的想法，并不是所有的代码都需要手撕，baseline is always there！

0x01 从策略梯度（Policy Gradient）到评判家（Critic）

1.1 回顾REINFORCE算法

从强化学习的三步范式出发：

第一步：通过运行策略$\Pi_\theta(a_t|s_t)$得到多个样本${\tau_i}$

第二步：根据采样样本（Sample）得到策略的梯度

∇𝜃𝐽(𝜃)=1𝑁Σ𝑖=1𝑁Σ𝑡=1𝑇[∇𝜃𝑙𝑜𝑔𝜋𝜃(𝑎𝑖,𝑡|𝑠𝑖,𝑡)][Σ𝑡′=𝑡𝑇𝑟(𝑠𝑡′𝑖,𝑎𝑡′𝑖)]

=∇𝜃𝐽(𝜃)=1𝑁Σ𝑖=1𝑁Σ𝑡=1𝑇[∇𝜃𝑙𝑜𝑔𝜋𝜃(𝑎𝑖,𝑡|𝑠𝑖,𝑡)][𝑄^𝑖,𝑡]

第三步：梯度上升

1.2 回顾梯度公式

梯度公式中的log项目在REINFORCEMENT中已经详细推导过，相当于是LIkelihood的一种加权；而后面的 $𝑄^𝑖,𝑡$ 代表的是我们在轨迹 $𝜏𝑖$ 中时间t中状态 $𝑠𝑖,𝑡$ 采取 $𝑎𝑖,𝑡$ 所得到的后续state- action期望奖励（excepted reward）；下面是真实的reward to go，注意和采样时候的区别CS285_Lecture06_Actor_Critic_Algorithms梯度公式中的log项目在REINFORCEMENT中已经详细推导过，相当于是LIkelihood的一种加权；而后面的 $𝑄^𝑖,𝑡$ 代表的是我们在轨迹$\tau_i$中时间t中状态 $𝑠𝑖,𝑡$ 采取 $𝑎𝑖,𝑡$ 所得到的后续state- action期望奖励（excepted reward）；下面是真实的reward to go，注意和采样时候的区别

（理论）（理论𝑠𝑡𝑎𝑡𝑒−𝑎𝑐𝑡𝑖𝑜𝑛−𝑣𝑎𝑙𝑢𝑒）𝑄(𝑠𝑡,𝑎𝑡)=Σ𝑡′=𝑡𝑇𝐸𝜋𝜃[𝑟(𝑠𝑡′,𝑎𝑡′)|𝑠𝑡,𝑎𝑡]

不要忘记我们的baseline，它可以起到降低方差的作用。我们可以将baseline加到REINFORCEMENT算法中。同时可以设置成为一个与状态有关的值，详细见上一个Lecture

（理论）（理论𝑠𝑡𝑎𝑡𝑒−𝑣𝑎𝑙𝑢𝑒）𝑉(𝑠𝑡)=𝐸𝑎𝑡−𝜋𝜃(𝑎𝑡|𝑠𝑡)𝑄(𝑠𝑡,𝑎𝑡)

以上是理论的推导

我们在实际采样中往往只能从有限的样本中得到，所以对于某个采样轨迹得到的梯度可以计算为：

注意这里的N代表的是总共有i个轨迹，采样和理论之间的区别，更近一步我们可以将：【某个状态下的动作总奖励】减去【某个状态下的所有动作期望】可以定义为这个【特定动作在该状态下的优势】

同样的和我们不知道Q和V一样，我们通常也不知道A的实际价值，但是我们使用近似（approximate）的方法来近似它，也就是我们的estimate return。通常如果我们的采样方式只是单纯的蒙特卡洛采样，我们得到的结果往往是：无偏差但是高方差的简单采样估计。

0x02 梯度评估（Policy Evaluation）

在上述我们可以看到在REINFORCEMENT里面对于policy gradient我们通常是使用【样本中特定的奖励求和】，这样带来的结果是因为我们采样的误差性导致最终结果具有high variance，这种情况下我们可能希望：

为什么不把这个函数拟合出来？——> value function fitting

如果我们希望拟合函数，上述的$Q(s,a),V(s),A(a,s)$中会选择哪个函数，可以看到

但是由于当前的状态我们知道，所以可以写成

因此我们可以得到在理论情况下原来的policy gradient为

在采样情况下

2.1 Policy evaluation based on Monte Carlo sampling

我们知道

所以我们的policy评价就是

如果我们只是从采样的方式来得到我们的估计，那么

虽然不想理论推导那样的优秀，但是同样是有效的。注意这里的过程是我们从REINFORCEMENT里面单纯的使用采样结果，转向构建一个state- based- function，我们需要做的是根据样本拟合这样的函数。但是注意这里！！我们有了dataset（input，output），或许我们可以使用监督学习（supervised learning）来使用一种神经网络的方法来学习一种函数关系。所以接下来问题是【我们如何从少量的样本中得到足够好的数据】

0x03 从Evaluation到Actor- Critic

3.1 批量AC算法（actor- critic algorithm）

image-20221031195007227

如果我们使用这样的算法，我们会发现其实在轨迹之间都可以对state- value进行评估，但是这样求解得到的y是不一样的，在不同轨迹中因为状态变换不一样，如果最后都达到station状态是可以的，但是对于不平稳是不OK的，因为我们的label不准确，所以我们可以增加一个discount factor

在这种情况下，如果我们采样Monte Carlo采样，计算梯度，哪一个是对的？

如果只是从option1采样，我们得到的结果是从每一步重新开始做discount，这个是符合直觉的

如果是从option2采样也不是没有结果的，如果我们针对未来恐惧所以会有很多的discount。

example：这里Sergey Levine尝试使用dead来解释option1和option2的区别，两者都是对的。

所以总结我们的算法，我们可以分为batcc AC与online AC两种方法

image-20221031200710794

0x04 演员评论算法 Actor- Critics Algorithm细节

4.1 拟合函数训练

我们可以选择用两个network来分别拟合state- value function与policy- state- action网络；但是在比较复杂的输入，比如游戏图片中我们往往需要使用convolution layer共享参数来减少网络的参数

4.2 在线AC训练

image-20221031201549764

如果只是这样训练，相当于我们每次更新梯度使用批量batchsize=1，所以非常差。我们从采样的角度出发，我们可以使用同步并行(synchronized parallel actor-critic) 或者异步平行（asynchronous parallel actor- critic）来多次采样，但是这样的损耗太大了，我们可以使用replay buffer来存储之前采样的数据。

但是如果我们只是简单的从replay buffer中得到train-data，但是这样是没有效果的，因为不是同一个轨迹构成的policy gradient是没有效果的，所以这样的算法是不对的。所以我们会尝试将之间的抽样得到的state- value转换成为包括Q(s,a)的值

image-20221031202523007

所以在这里我们不再使用state- value，而是使用action- state- value

4.3 Baseline设置

我们在Policy gradient引入一个常数，得到无偏差、但是高方差的梯度；在AC中我们使用 r+V（t+1）- V（t）来得到评估，这样会有一个低方差但是有偏的方程，所以我们如何在拟合价值函数过程中得到我们的梯度，也就是用Q-V来评估（称为蒙特卡洛方法），但是这样对采样数量要求高。

我们可以考虑使用某种方式来结合两者，也就是采样N-step returns

之后包括generalized advantage estimation推导可以发现$\gamma$可以有效的降低方差

0x05 review

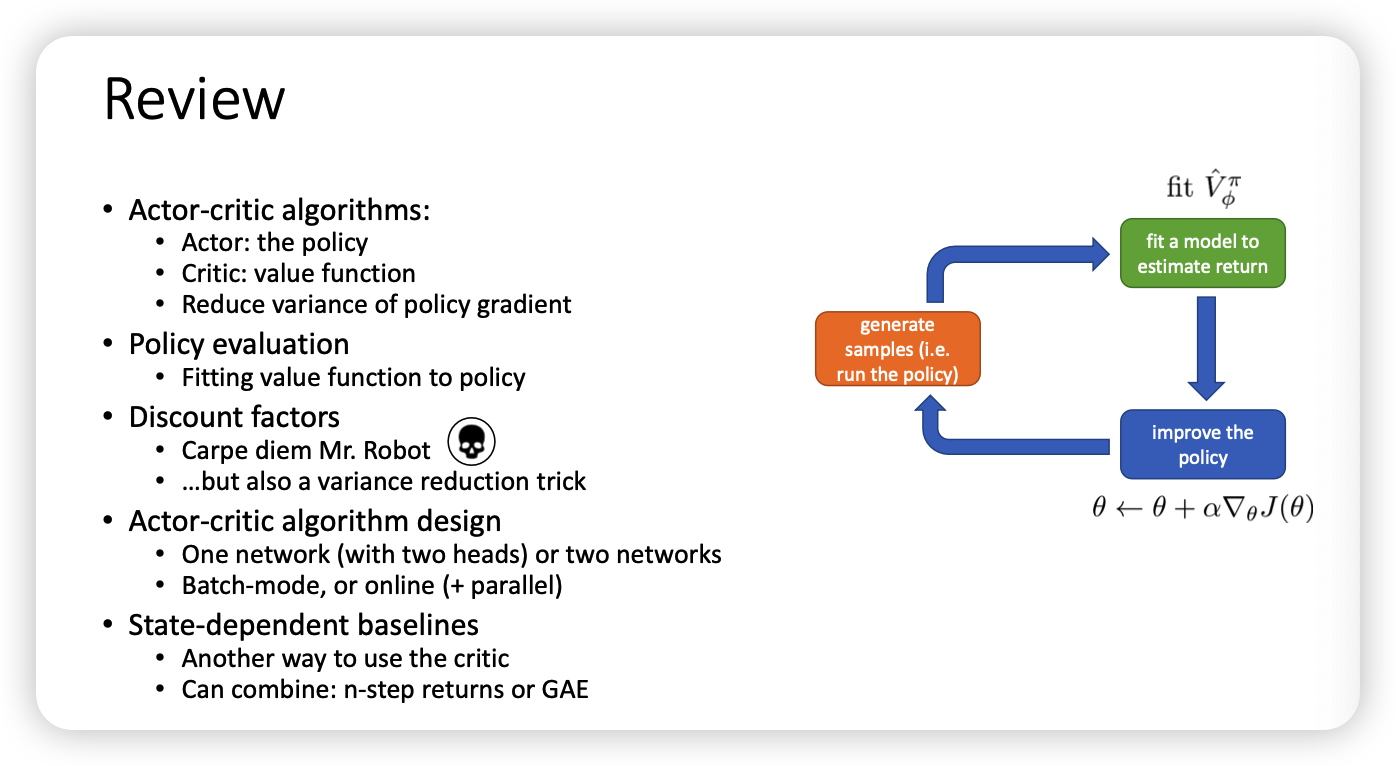
image-20221031203538556

0x06 code

参考动手学强化学习

import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
import rl_utils
class ActorCritic:
    def __init__(self, state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
                 gamma, device):
        # 策略网络
        self.actor = PolicyNet(state_dim, hidden_dim, action_dim).to(device)
        self.critic = ValueNet(state_dim, hidden_dim).to(device)  # 价值网络
        # 策略网络优化器
        self.actor_optimizer = torch.optim.Adam(self.actor.parameters(),
                                                lr=actor_lr)
        self.critic_optimizer = torch.optim.Adam(self.critic.parameters(),
                                                 lr=critic_lr)  # 价值网络优化器
        self.gamma = gamma
        self.device = device

    def take_action(self, state):
        state = torch.tensor([state], dtype=torch.float).to(self.device)
        probs = self.actor(state)
        action_dist = torch.distributions.Categorical(probs)
        action = action_dist.sample()
        return action.item()

    def update(self, transition_dict):
        states = torch.tensor(transition_dict['states'],
                              dtype=torch.float).to(self.device)
        actions = torch.tensor(transition_dict['actions']).view(-1, 1).to(
            self.device)
        rewards = torch.tensor(transition_dict['rewards'],
                               dtype=torch.float).view(-1, 1).to(self.device)
        next_states = torch.tensor(transition_dict['next_states'],
                                   dtype=torch.float).to(self.device)
        dones = torch.tensor(transition_dict['dones'],
                             dtype=torch.float).view(-1, 1).to(self.device)

        # 时序差分目标
        td_target = rewards + self.gamma * self.critic(next_states) * (1 -
                                                                       dones)
        td_delta = td_target - self.critic(states)  # 时序差分误差
        log_probs = torch.log(self.actor(states).gather(1, actions))
        actor_loss = torch.mean(-log_probs * td_delta.detach())
        # 均方误差损失函数
        critic_loss = torch.mean(
            F.mse_loss(self.critic(states), td_target.detach()))
        self.actor_optimizer.zero_grad()
        self.critic_optimizer.zero_grad()
        actor_loss.backward()  # 计算策略网络的梯度
        critic_loss.backward()  # 计算价值网络的梯度
        self.actor_optimizer.step()  # 更新策略网络的参数
        self.critic_optimizer.step()  # 更新价值网络的参数
  actor_lr = 1e-3
critic_lr = 1e-2
num_episodes = 1000
hidden_dim = 128
gamma = 0.98
device = torch.device("cuda") if torch.cuda.is_available() else torch.device(
    "cpu")

env_name = 'CartPole-v0'
env_name='MountainCar-v0'
env = gym.make(env_name)
env.seed(0)
torch.manual_seed(0)
state_dim = env.observation_space.shape[0]
action_dim = env.action_space.n
agent = ActorCritic(state_dim, hidden_dim, action_dim, actor_lr, critic_lr,
                    gamma, device)

return_list = rl_utils.train_on_policy_agent(env, agent, num_episodes)
episodes_list = list(range(len(return_list)))
plt.plot(episodes_list, return_list)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()

mv_return = rl_utils.moving_average(return_list, 9)
plt.plot(episodes_list, mv_return)
plt.xlabel('Episodes')
plt.ylabel('Returns')
plt.title('Actor-Critic on {}'.format(env_name))
plt.show()

image-20221031233251437