CS285 深度强化学习 Vol5 ｜ Policy gradient

本节课的目标是搞明白Policy gradient一类的REINFORCEMENT方法，并且理解背后的局限性，然后知道为什么textbook很容易讲清楚，但是在实践中不行的原因。之后从Causality和Baseline两种方法来降低On- policy PG的方差。并给出结合IS（important sampling）的Off policy的梯度方法。最后利用代码实现RL里面的hello world—CartPole-v0来实现。

01 什么是Policy gradients

1.1 PG的梯度函数的下载

回顾DRL的目标，我们需要的是增加累积奖励的期望：

（目标函数）（目标函数）𝑚𝑎𝑥 𝐸𝜏−𝑝𝜃(𝜏)[Σ𝑡𝑟(𝑠𝑡,𝑎𝑡)]

根据$(s_t,a_t)$ 对的马尔可夫性质，(在有限的情况下finite horizon case）下简化成为

𝑚𝑎𝑥 Σ𝑡=1𝑇𝐸(𝑠𝑡,𝑎𝑡)−𝑝𝜃(𝑠𝑡,𝑎𝑡)[𝑟(𝑠𝑡,𝑎𝑡)]

因此我们可以根据$\pi_\theta$采样N个$\tau$,然后求得期望为

（采样后的目标函数）（采样后的目标函数）𝐽(𝜃)=1𝑁Σ𝑖Σ𝑡𝑟(𝑠𝑖,𝑡,𝑎𝑖,𝑡)

这个式子的重要意义在于它直接给我们反应当前policy的优劣，也指明了我们需要前进的方向，就是最大化这个期望，虽然有的时候这个式子并不是容易计算。但是请把哪些问题先放放，直观的最大化这个问题，也就是用梯度提升的方法：

（上式简写）𝐽(𝜃)=∫𝑝𝜃(𝜏)𝑟(𝜏)𝑑𝜏（上式简写）

那么对参数求导的结果就是；同时由于我们无法直接取值函数，我们通常需要转换为期望的方式来利用sampling—expectation的方式来求期望

（目标函数梯度）（目标函数梯度）∇𝜃𝐽(𝜃)=∫∇𝜃𝑝𝜃(𝜏)∗𝑟(𝜏)𝑑𝜏)=∫𝑝𝜃(𝜏)∗∇𝜃𝑙𝑜𝑔𝑝𝜃(𝜏)∗𝑟(𝜏)𝑑𝜏=𝐸𝜏−𝑝𝜃(𝜏)[∇𝜃𝑙𝑜𝑔𝑝𝜃(𝜏)∗𝑟(𝜏)]

我们对上面的目标函数更进一步的探讨；首先疑问就是什么是$p_\theta(\tau)$,在MDP的state- observation-action- state转移中我们可以认识到

𝑝𝜃(𝜏)=𝑝(𝑠1)∏𝜋𝜃(𝑎𝑡|𝑠𝑡)𝑝(𝑠𝑡+1|𝑠𝑡,𝑎𝑡)

所以可以很轻松的替换掉上述

𝑙𝑜𝑔𝑝𝜃(𝜏)=𝑙𝑜𝑔𝑝(𝑠1)+Σ𝑙𝑜𝑔𝜋𝜃(𝑎𝑡|𝑠𝑡)+𝑙𝑜𝑔𝑝(𝑠𝑡+1|𝑠𝑡,𝑎𝑡)

假设我们求导的化，那么目标函数梯度就会变成

Stop to think : just like before we evaluated our reinforcement learning objective by generating samples by actually running our policy in the world to get an estimate of an exception

这样情况下我们就可以得到采样的后的梯度计算：

虽然我们成功得到了，我们如何从采样结果中得到如何计算梯度；但是我们需要对分析它具体的含义。

1.2 理解PG含义

我们可以看到损失函数内部主要有两部分组成，第一部分是有梯度的东西，第二部份是奖励的求和；那么对于两项分别分析，可以发现第一部分梯度与简单的MLE类似，也就是直接的梯度下降，但是由于有奖励的加权，导致我们的结果是：

good stuff is made more likely;bad stuff is made less likely（增加好的可能性，降低坏的可能性），也标记为“trial and error”

对于中间的一项， ,假设我们用一个神经网络来进行拟合，假如采用Gaussian policies；也就是我们的模型假设是

那么我们的损失函数，根据MLE自然而然就可以得到(参考linear regression）

这样我们就得到我们的REINFORCEMENT algorithm；这里缩写是针对：REward Increments=nonnegative FactorOffset Reinforcement Characteristic+Eligibility

image-20221026121451902

但是PG的问题在于：

1. 我们是否可以在partial observation，也就是o不等于s情况下使用？
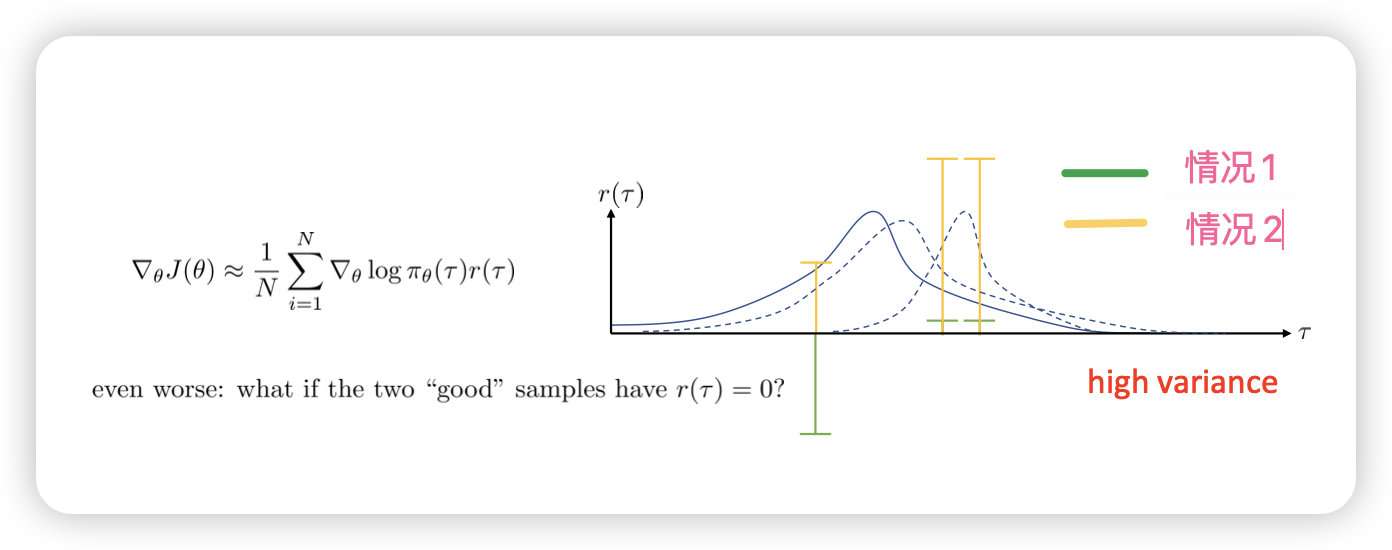
2. 具有很大的方差，对于不同的reward取值结果大不相同。
3. example：假设N=3；其中总的奖励分为与（一负，两正），那么更新后的策略会偏向于右边，假如是加上constant（三正），那么更新的策略会比偏向中间。这种不确定性导致最终结果的方差偏大

image-20221026121503952

0x02 如何降低方差一：Causality

在未来发生的事情并不会对现在的事情造成影响（policy at time b cannot affect reward at time a when a<b）,因此在t之前的梯度不会对后面造成影响

所以我们的梯度需要：

变成；注意后面计算奖励的下标！有效的证明过程可能需要在paper中才能看到

通常的我们会将后面的记为：reward to go：

0x03 如何降低发差二：Baselines

首先直觉的感受不同reward的影响，还是之前的例子，如果reward=(-1,2,2)和（1，4，4）或者是（10000，10005，10005）这样计算的结果通常是不一样的。我们需要在其中减去一个baseline，相当于unbiased in expectation，很直观的我们是减去奖励的平均值，注意！！平均值不一定是最好的

可以简单的证明减去一个baseline不会对梯度造成影响，但是会对梯度变化程度造成影响

除去平均值，我们会采取什么baseline来计算？我们的目标是降低模型的方差，那么最好的baseline就是让模型方差最低的，根据方差计算

那么

直接对方差Var的bias求导

这样就可以得到最好的b值，但是通常在实践中很难计算，所以还君之好用

0x04 Off-policy Policy gradient

我们在之前的讨论中得到最终的梯度理论公式和采样公式，但是我们仔细思考这个过程，我们需要第i次采样得到完整 之后才能利用梯度提升更新policy，这样对于每次policy只是简单的更新一次梯度；这样的结果就是采样效率非常低。

image-20221026121521658

可以简单的引入 important sampling；来尝试解决这个问题，其理论过程是这样的

这样的好处是我们可以使用智能体旧策略 来更新策略梯度的值,得到 ,也就是目标函数会变成

之间的比值可以展开得到

因此可以得到 Important sampling下的目标函数的期望

继续我们之前的causality的说明，所以采样情况下上面展开得到

通常reward to go里的分布会删掉，因此不影响结果（paper中有）

同时可以改变策略的比值，这个在之后课程中会讲到,这里采用first- order approximation，

因此得到Off-Policy Policy gradient with important sampling的目标函数梯度：

作为对比之前的on- policy gradient是：

0x05 代码实现

参考《动手学深度学习》

首先几个有趣的发现

1. 在CartPole-v0成功的不一定能在MountainCar-v0中实现，这个与奖励函数的设置关系很大（小车没有上山之前都是-1，被打击到了）
2. 不同的超参数对最终结果影响很大
3. 推荐使用GYM 0.21版本；最新版本总会出问题

5.1 环境搭建

## 环境说明：Cartpole-v0 
我们采用的测试环境是 CartPole-v0，其状态空间相对简单，只有 4 个变量，因此网络结构
的设计也相对简单：采用一层 128 个神经元的全连接并以 ReLU 作为激活函数。当遇到更复
杂的诸如以图像作为输入的环境时，我们可以考虑采用深度卷积神经网络。
# 引入一些包
from pyvirtualdisplay import Display
display = Display(visible=0, size=(1400, 900))
display.start()

import matplotlib.pyplot as plt
from IPython import display
import time
from IPython import display
from PIL import Image
import gym
import torch
import torch.nn.functional as F
import numpy as np
import matplotlib.pyplot as plt
from tqdm import tqdm

5.2 定义Policy net

输入是state，输出是action。随便一个浅层MLP就够了

class PolicyNet(torch.nn.Module):
    def __init__(self,state_dim,hidden_dim,action_dim):
        super(PolicyNet,self).__init__()
        self.fc1=torch.nn.Linear(state_dim,hidden_dim)
        self.fc2=torch.nn.Linear(hidden_dim,action_dim)
        for m in self.modules():
            if isinstance(m, torch.nn.Linear):
                torch.nn.init.normal_(m.weight, std=0.01)

    def forward(self,x):
        x=F.relu(self.fc1(x))
        return F.softmax(self.fc2(x),dim=1)

5.3 定义算法

三步，首先sample generation、然后policy evaluate，之后是improve policy

from traitlets import observe

class REINFORCE:
    def __init__(self,state_dim,hidden_dim,action_dim,learning_rate,gamma,device):
        self.policy_net=PolicyNet(state_dim,hidden_dim,action_dim).to(device)
        self.optimizer=torch.optim.Adam(self.policy_net.parameters(),lr=learning_rate)
        self.gamma=gamma
        self.device=device

    def take_action(self,state):
        # 根据动作概率分布随机采样
        state=torch.tensor([state],dtype=torch.float).to(self.device)
        probs=self.policy_net(state)
        action_dist=torch.distributions.Categorical(probs)
        action=action_dist.sample()
        return action.item()

    def update(self,transition_dict):
        reward_list=transition_dict['rewards']
        state_list=transition_dict['states']
        action_list=transition_dict['actions']

        G=0
        self.optimizer.zero_grad()
        for i in reversed(range(len(reward_list))):
            # 从最后一步开始
            state=torch.tensor([state_list[i]],dtype=torch.float).to(self.device)
            reward=reward_list[i]
            action=torch.tensor([action_list[i]]).view(-1,1).to(self.device)
            log_prob=torch.log(self.policy_net(state).gather(1,action))
            G=self.gamma*G+reward
            loss=-log_prob*G
            loss.backward()
        self.optimizer.step()

5.3 开始实验

learning_rate=0.001
num_episodes=1000
hidden_dim=128
gamma=0.98
device=torch.device('cuda' if torch.cuda.is_available() else 'cpu')
env_name='CartPole-v0'
# env_name='MountainCar-v0'
# env_name='LunarLander-v2'
## 观察环境

env=gym.make(env_name)
env.seed(0)
print('state:{}'.format(env.observation_space.dtype))
print('action:{}'.format(env.action_space))
print('state shape:{}~{}'.format(env.observation_space.low,env.observation_space.high))
torch.manual_seed(0)
state_dim=env.observation_space.shape[0]
action_dim=env.action_space.n
agent=REINFORCE(state_dim,hidden_dim,action_dim,learning_rate,gamma,device)
return_list = []
for i in range(10):
    with tqdm(total=int(num_episodes / 10), desc='Iteration %d' % i) as pbar:
        for i_episode in range(int(num_episodes / 10)):
            episode_return = 0
            transition_dict = {
                'states': [],
                'actions': [],
                'next_states': [],
                'rewards': [],
                'dones': []
            }

            state = env.reset()
            # 清除当前 Cell 的输出
            done = False
            while not done:
                action = agent.take_action(state)
                next_state, reward, done, _ = env.step(action)
                transition_dict['states'].append(state)
                transition_dict['actions'].append(action)
                transition_dict['next_states'].append(next_state)
                # special for Mountain
                # reward=(next_state[0]+1)**5
                # if abs(next_state[1])>0.04:
                #     reward+=1
                transition_dict['rewards'].append(reward)
                transition_dict['dones'].append(done)
                state = next_state
                episode_return += reward
            return_list.append(episode_return)
            agent.update(transition_dict)
            if (i_episode + 1) % 10 == 0:
                pbar.set_postfix({
                    'episode':
                    '%d' % (num_episodes / 10 * i + i_episode + 1),
                    'return':
                    '%.3f' % np.mean(return_list[-10:])
                })
            pbar.update(1)

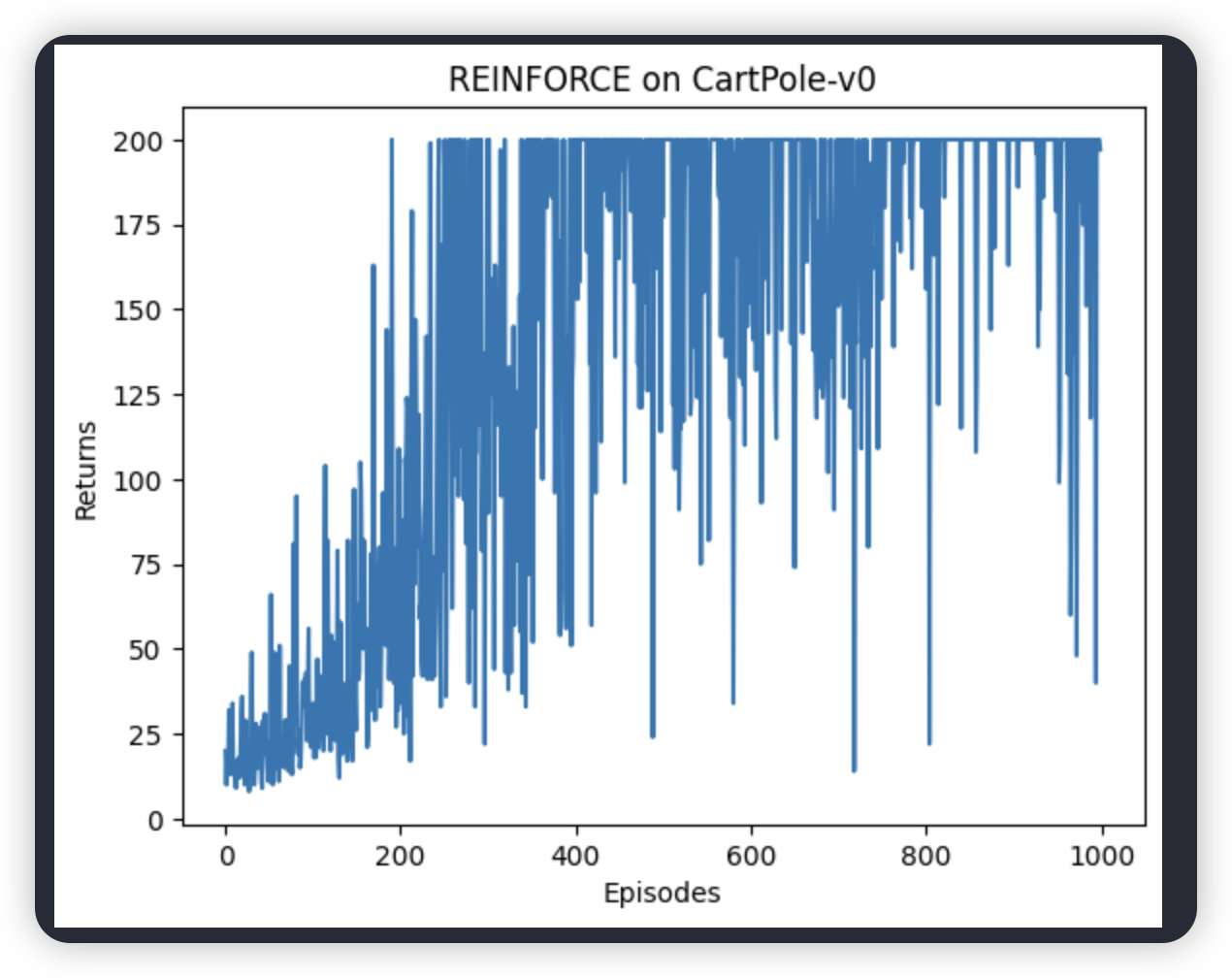
假如设置三层网络结果有点奇怪，但是policy是好的

两层结果

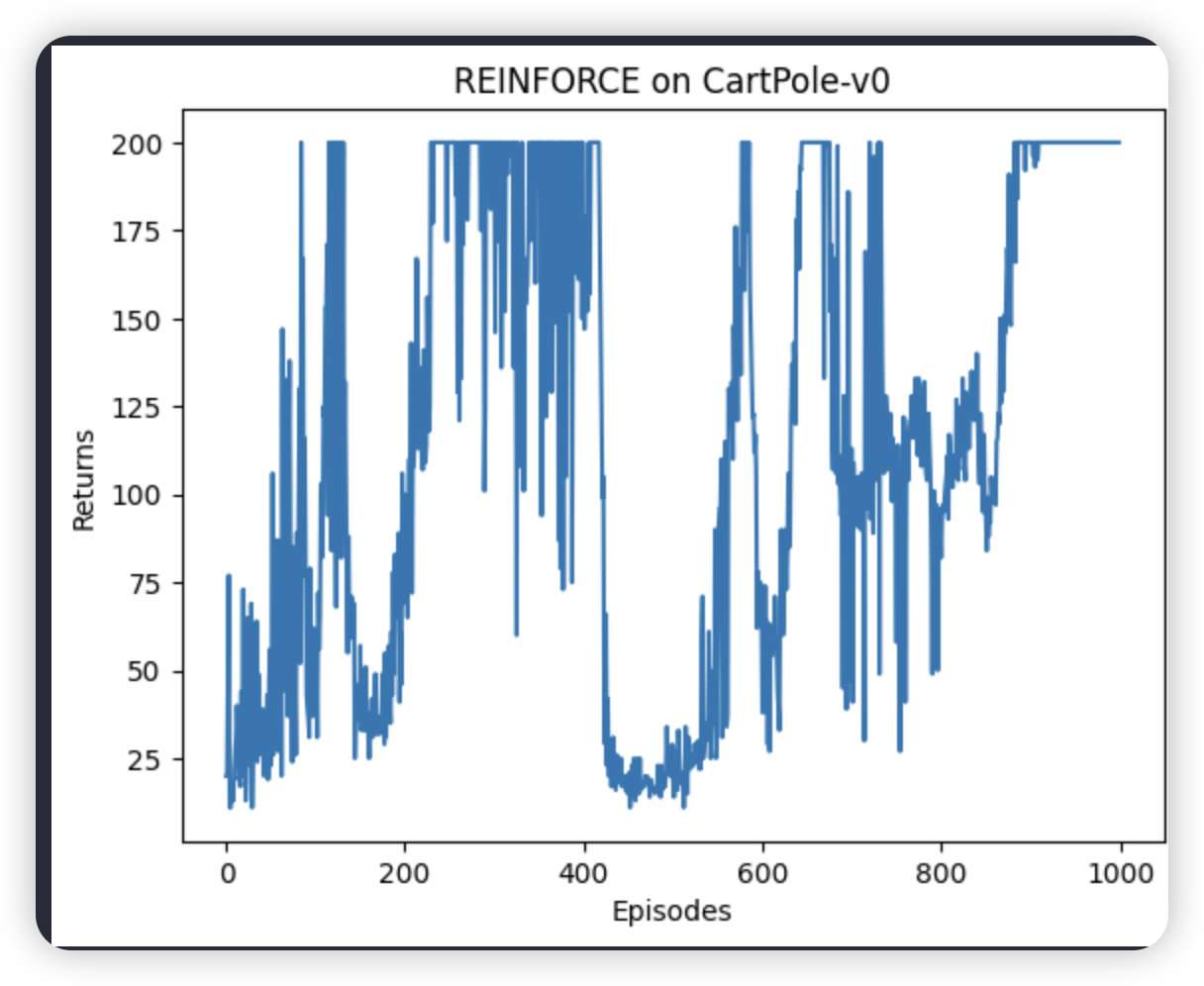
三层神经网络，但是policy好的

5.4 观察

done = False
state = env.reset()
flag=1
    # 防止刷新过快
while flag<100:
    action = agent.take_action(state)
    next_state, reward, done, _ = env.step(action)
    state=next_state
    # 清除当前 Cell 的输出
    display.clear_output(wait=True)
    # 渲染画面，得到画面的像素数组
    rgb_array = env.render(mode='rgb_array')
    # 使用像素数组生成图片
    img = Image.fromarray(rgb_array)
    # 当前 Cell 中展示图片
    display.display(img)
    time.sleep(1/24)
    flag+=1

第一个是2层，第二是3层

视频可以看

上传视频封面

两层网络情况

上传视频封面

三层网络情况